49 | 搜索：如何用A*搜索算法实现游戏中的寻路功能？

魔兽世界、仙剑奇侠传这类 MMRPG 游戏，不知道你有没有玩过？在这些游戏中，有一个非常重要的功能，那就是人物角色自动寻路。当人物处于游戏地图中的某个位置的时候，我们用鼠标点击另外一个相对较远的位置，人物就会自动地绕过障碍物走过去。玩过这么多游戏，不知你是否思考过，这个功能是怎么实现的呢？

算法解析

实际上，这是一个非常典型的搜索问题。人物的起点就是他当下所在的位置，终点就是鼠标点击的位置。我们需要在地图中，找一条从起点到终点的路径。这条路径要绕过地图中所有障碍物，并且看起来要是一种非常聪明的走法。所谓“聪明”，笼统地解释就是，走的路不能太绕。理论上讲，最短路径显然是最聪明的走法，是这个问题的最优解。

不过，在第 44 节最优出行路线规划问题中，我们也讲过，如果图非常大，那 Dijkstra 最短路径算法的执行耗时会很多。在真实的软件开发中，我们面对的是超级大的地图和海量的寻路请求，算法的执行效率太低，这显然是无法接受的。

实际上，像出行路线规划、游戏寻路，这些真实软件开发中的问题，一般情况下，我们都不需要非得求最优解（也就是最短路径）。在权衡路线规划质量和执行效率的情况下，我们只需要寻求一个次优解就足够了。那如何快速找出一条接近于最短路线的次优路线呢？

这个快速的路径规划算法，就是我们今天要学习的A* 算法。实际上，A* 算法是对 Dijkstra 算法的优化和改造。如何将 Dijkstra 算法改造成 A* 算法呢？为了更好地理解接下来要讲的内容，我建议你先温习下第 44 节中的 Dijkstra 算法的实现原理。

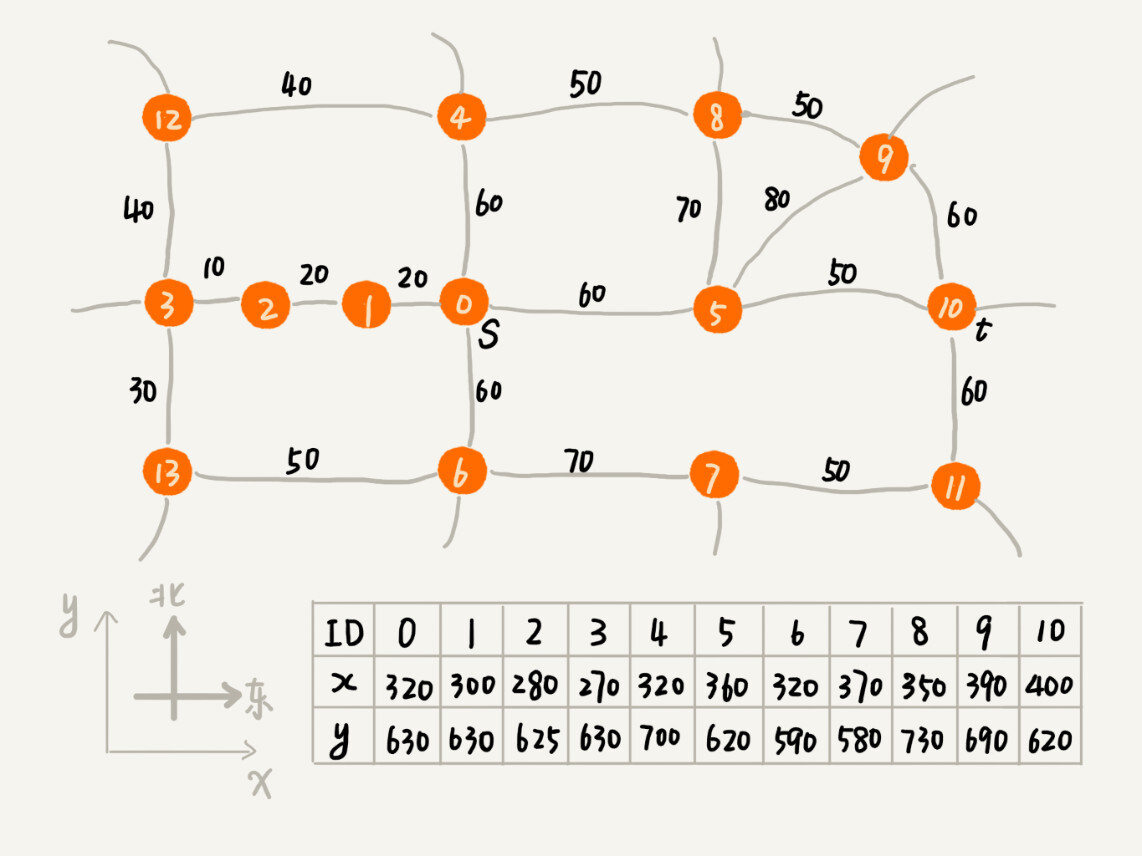
Dijkstra 算法有点儿类似 BFS 算法，它每次找到跟起点最近的顶点，往外扩展。这种往外扩展的思路，其实有些盲目。为什么这么说呢？我举一个例子来给你解释一下。下面这个图对应一个真实的地图，每个顶点在地图中的位置，我们用一个二维坐标（x，y）来表示，其中，x 表示横坐标，y 表示纵坐标。

在 Dijkstra 算法的实现思路中，我们用一个优先级队列，来记录已经遍历到的顶点以及这个顶点与起点的路径长度。顶点与起点路径长度越小，就越先被从优先级队列中取出来扩展，从图中举的例子可以看出，尽管我们找的是从 s 到 t 的路线，但是最先被搜索到的顶点依次是 1，2，3。通过肉眼来观察，这个搜索方向跟我们期望的路线方向（s 到 t 是从西向东）是反着的，路线搜索的方向明显“跑偏”了。

之所以会“跑偏”，那是因为我们是按照顶点与起点的路径长度的大小，来安排出队列顺序的。与起点越近的顶点，就会越早出队列。我们并没有考虑到这个顶点到终点的距离，所以，在地图中，尽管 1，2，3 三个顶点离起始顶点最近，但离终点却越来越远。

如果我们综合更多的因素，把这个顶点到终点可能还要走多远，也考虑进去，综合来判断哪个顶点该先出队列，那是不是就可以避免“跑偏”呢？

当我们遍历到某个顶点的时候，从起点走到这个顶点的路径长度是确定的，我们记作 g(i)（i 表示顶点编号）。但是，从这个顶点到终点的路径长度，我们是未知的。虽然确切的值无法提前知道，但是我们可以用其他估计值来代替。

这里我们可以通过这个顶点跟终点之间的直线距离，也就是欧几里得距离，来近似地估计这个顶点跟终点的路径长度（注意：路径长度跟直线距离是两个概念）。我们把这个距离记作 h(i)（i 表示这个顶点的编号），专业的叫法是启发函数（heuristic function）。因为欧几里得距离的计算公式，会涉及比较耗时的开根号计算，所以，我们一般通过另外一个更加简单的距离计算公式，那就是曼哈顿距离（Manhattan distance）。曼哈顿距离是两点之间横纵坐标的距离之和。计算的过程只涉及加减法、符号位反转，所以比欧几里得距离更加高效。

int hManhattan(Vertex v1, Vertex v2) { // Vertex 表示顶点，后面有定义
  return Math.abs(v1.x - v2.x) + Math.abs(v1.y - v2.y);
}
复制代码

原来只是单纯地通过顶点与起点之间的路径长度 g(i)，来判断谁先出队列，现在有了顶点到终点的路径长度估计值，我们通过两者之和 f(i)=g(i)+h(i)，来判断哪个顶点该最先出队列。综合两部分，我们就能有效避免刚刚讲的“跑偏”。这里 f(i) 的专业叫法是估价函数（evaluation function）。

从刚刚的描述，我们可以发现，A* 算法就是对 Dijkstra 算法的简单改造。实际上，代码实现方面，我们也只需要稍微改动几行代码，就能把 Dijkstra 算法的代码实现，改成 A* 算法的代码实现。

在 A* 算法的代码实现中，顶点 Vertex 类的定义，跟 Dijkstra 算法中的定义，稍微有点儿区别，多了 x，y 坐标，以及刚刚提到的 f(i) 值。图 Graph 类的定义跟 Dijkstra 算法中的定义一样。为了避免重复，我这里就没有再贴出来了。

private class Vertex {
  public int id; // 顶点编号 ID
  public int dist; // 从起始顶点，到这个顶点的距离，也就是 g(i)
  public int f; // 新增：f(i)=g(i)+h(i)
  public int x, y; // 新增：顶点在地图中的坐标（x, y）
  public Vertex(int id, int x, int y) {
    this.id = id;
    this.x = x;
    this.y = y;
    this.f = Integer.MAX_VALUE;
    this.dist = Integer.MAX_VALUE;
  }
}
// Graph 类的成员变量，在构造函数中初始化
Vertex[] vertexes = new Vertex[this.v];
// 新增一个方法，添加顶点的坐标
public void addVetex(int id, int x, int y) {
  vertexes[id] = new Vertex(id, x, y)
}
复制代码

A* 算法的代码实现的主要逻辑是下面这段代码。它跟 Dijkstra 算法的代码实现，主要有 3 点区别：

• 优先级队列构建的方式不同。A* 算法是根据 f 值（也就是刚刚讲到的 f(i)=g(i)+h(i)）来构建优先级队列，而 Dijkstra 算法是根据 dist 值（也就是刚刚讲到的 g(i)）来构建优先级队列；

• A* 算法在更新顶点 dist 值的时候，会同步更新 f 值；

• 循环结束的条件也不一样。Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。

public void astar(int s, int t) { // 从顶点 s 到顶点 t 的路径
  int[] predecessor = new int[this.v]; // 用来还原路径
  // 按照 vertex 的 f 值构建的小顶堆，而不是按照 dist
  PriorityQueue queue = new PriorityQueue(this.v);
  boolean[] inqueue = new boolean[this.v]; // 标记是否进入过队列
  vertexes[s].dist = 0;
  vertexes[s].f = 0;
  queue.add(vertexes[s]);
  inqueue[s] = true;
  while (!queue.isEmpty()) {
    Vertex minVertex = queue.poll(); // 取堆顶元素并删除
    for (int i = 0; i < adj[minVertex.id].size(); ++i) {
      Edge e = adj[minVertex.id].get(i); // 取出一条 minVetex 相连的边
      Vertex nextVertex = vertexes[e.tid]; // minVertex-->nextVertex
      if (minVertex.dist + e.w < nextVertex.dist) { // 更新 next 的 dist,f
        nextVertex.dist = minVertex.dist + e.w;
        nextVertex.f 
           = nextVertex.dist+hManhattan(nextVertex, vertexes[t]);
        predecessor[nextVertex.id] = minVertex.id;
        if (inqueue[nextVertex.id] == true) {
          queue.update(nextVertex);
        } else {
          queue.add(nextVertex);
          inqueue[nextVertex.id] = true;
        }
      }
      if (nextVertex.id == t) { // 只要到达 t 就可以结束 while 了
        queue.clear(); // 清空 queue，才能推出 while 循环
        break; 
      }
    }
  }
  // 输出路径
  System.out.print(s);
  print(s, t, predecessor); // print 函数请参看 Dijkstra 算法的实现
}
复制代码

尽管 A* 算法可以更加快速的找到从起点到终点的路线，但是它并不能像 Dijkstra 算法那样，找到最短路线。这是为什么呢？

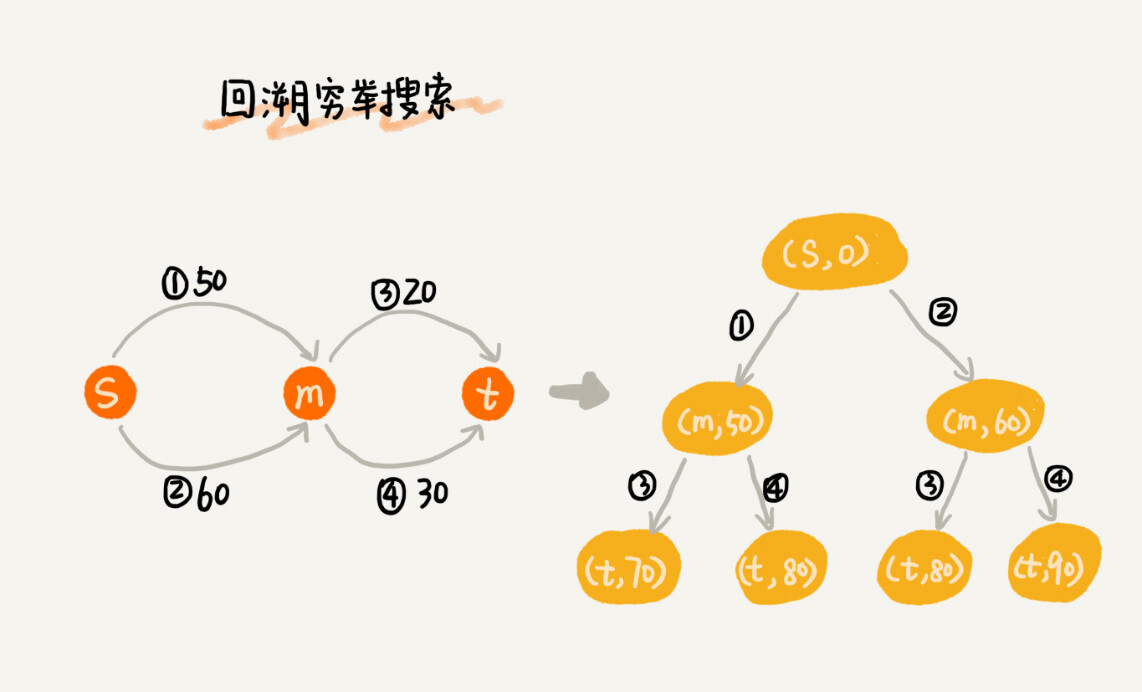
要找出起点 s 到终点 t 的最短路径，最简单的方法是，通过回溯穷举所有从 s 到达 t 的不同路径，然后对比找出最短的那个。不过很显然，回溯算法的执行效率非常低，是指数级的。

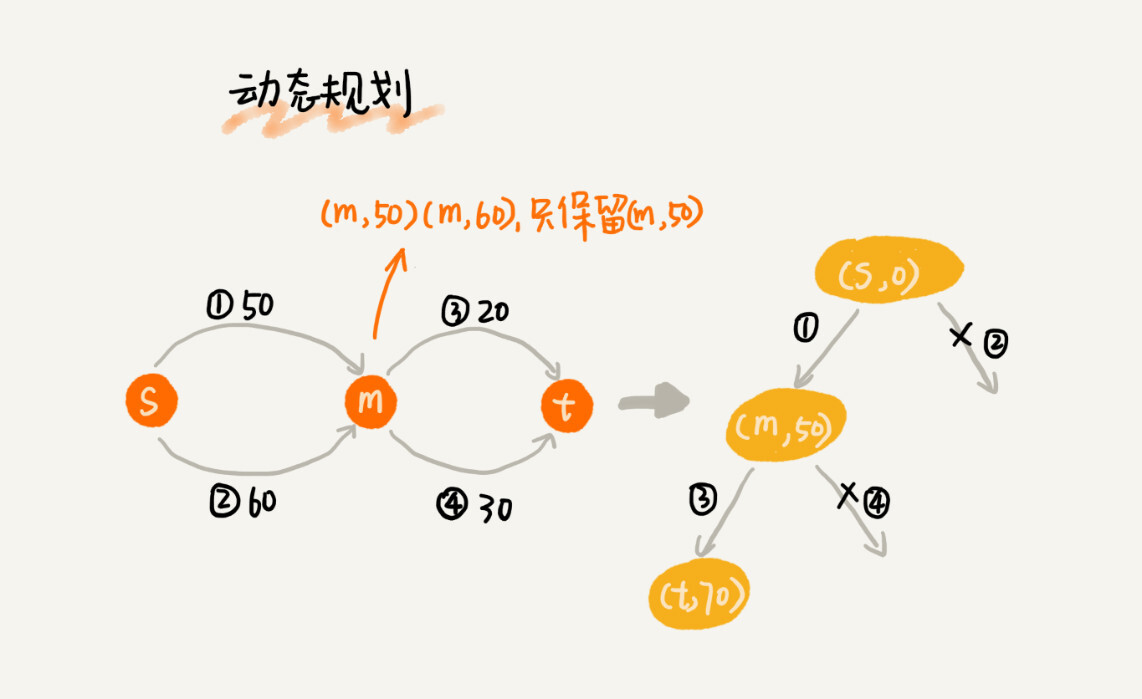
Dijkstra 算法在此基础之上，利用动态规划的思想，对回溯搜索进行了剪枝，只保留起点到某个顶点的最短路径，继续往外扩展搜索。动态规划相较于回溯搜索，只是换了一个实现思路，但它实际上也考察到了所有从起点到终点的路线，所以才能得到最优解。

A* 算法之所以不能像 Dijkstra 算法那样，找到最短路径，主要原因是两者的 while 循环结束条件不一样。刚刚我们讲过，Dijkstra 算法是在终点出队列的时候才结束，A* 算法是一旦遍历到终点就结束。对于 Dijkstra 算法来说，当终点出队列的时候，终点的 dist 值是优先级队列中所有顶点的最小值，即便再运行下去，终点的 dist 值也不会再被更新了。对于 A* 算法来说，一旦遍历到终点，我们就结束 while 循环，这个时候，终点的 dist 值未必是最小值。

A* 算法利用贪心算法的思路，每次都找 f 值最小的顶点出队列，一旦搜索到终点就不在继续考察其他顶点和路线了。所以，它并没有考察所有的路线，也就不可能找出最短路径了。

搞懂了 A* 算法，我们再来看下，如何借助 A* 算法解决今天的游戏寻路问题？

要利用 A* 算法解决这个问题，我们只需要把地图，抽象成图就可以了。不过，游戏中的地图跟第 44 节中讲的我们平常用的地图是不一样的。因为游戏中的地图并不像我们现实生活中那样，存在规划非常清晰的道路，更多的是宽阔的荒野、草坪等。所以，我们没法利用 44 节中讲到的抽象方法，把岔路口抽象成顶点，把道路抽象成边。

实际上，我们可以换一种抽象的思路，把整个地图分割成一个一个的小方块。在某一个方块上的人物，只能往上下左右四个方向的方块上移动。我们可以把每个方块看作一个顶点。两个方块相邻，我们就在它们之间，连两条有向边，并且边的权值都是 1。所以，这个问题就转化成了，在一个有向有权图中，找某个顶点到另一个顶点的路径问题。将地图抽象成边权值为 1 的有向图之后，我们就可以套用 A* 算法，来实现游戏中人物的自动寻路功能了。

总结引申

我们今天讲的 A* 算法属于一种启发式搜索算法（Heuristically Search Algorithm）。实际上，启发式搜索算法并不仅仅只有 A* 算法，还有很多其他算法，比如 IDA* 算法、蚁群算法、遗传算法、模拟退火算法等。如果感兴趣，你可以自行研究下。

启发式搜索算法利用估价函数，避免“跑偏”，贪心地朝着最有可能到达终点的方向前进。这种算法找出的路线，并不是最短路线。但是，实际的软件开发中的路线规划问题，我们往往并不需要非得找最短路线。所以，鉴于启发式搜索算法能很好地平衡路线质量和执行效率，它在实际的软件开发中的应用更加广泛。实际上，在第 44 节中，我们讲到的地图 App 中的出行路线规划问题，也可以利用启发式搜索算法来实现。

课后思考

我们之前讲的“迷宫问题”是否可以借助 A* 算法来更快速地找到一个走出去的路线呢？如果可以，请具体讲讲该怎么来做；如果不可以，请说说原因。

欢迎留言和我分享，也欢迎点击“请朋友读”，把今天的内容分享给你的好友，和他一起讨论、学习。