41 | 动态规划理论:一篇文章带你彻底搞懂最优子结构、无后效性和重复子问题

讲述:修阳
时长16:23大小15.01M
上一节,我通过两个非常经典的问题,向你展示了用动态规划解决问题的过程。现在你对动态规划应该有了一个初步的认识。
今天,我主要讲动态规划的一些理论知识。学完这节内容,可以帮你解决这样几个问题:什么样的问题可以用动态规划解决?解决动态规划问题的一般思考过程是什么样的?贪心、分治、回溯、动态规划这四种算法思想又有什么区别和联系?
理论的东西都比较抽象,不过你不用担心,我会结合具体的例子来讲解,争取让你这次就能真正理解这些知识点,也为后面的应用和实战做好准备。
“一个模型三个特征”理论讲解
什么样的问题适合用动态规划来解决呢?换句话说,动态规划能解决的问题有什么规律可循呢?实际上,动态规划作为一个非常成熟的算法思想,很多人对此已经做了非常全面的总结。我把这部分理论总结为“一个模型三个特征”。
首先,我们来看,什么是“一个模型”?它指的是动态规划适合解决的问题的模型。我把这个模型定义为“多阶段决策最优解模型”。下面我具体来给你讲讲。
我们一般是用动态规划来解决最优问题。而解决问题的过程,需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后我们寻找一组决策序列,经过这组决策序列,能够产生最终期望求解的最优值。
现在,我们再来看,什么是“三个特征”?它们分别是最优子结构、无后效性和重复子问题。这三个概念比较抽象,我来逐一详细解释一下。
1. 最优子结构
最优子结构指的是,问题的最优解包含子问题的最优解。反过来说就是,我们可以通过子问题的最优解,推导出问题的最优解。如果我们把最优子结构,对应到我们前面定义的动态规划问题模型上,那我们也可以理解为,后面阶段的状态可以通过前面阶段的状态推导出来。
2. 无后效性
无后效性有两层含义,第一层含义是,在推导后面阶段的状态的时候,我们只关心前面阶段的状态值,不关心这个状态是怎么一步一步推导出来的。第二层含义是,某阶段状态一旦确定,就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型,其实基本上都会满足无后效性。
3. 重复子问题
这个概念比较好理解。前面一节,我已经多次提过。如果用一句话概括一下,那就是,不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态。
“一个模型三个特征”实例剖析
“一个模型三个特征”这部分是理论知识,比较抽象,你看了之后可能还是有点懵,有种似懂非懂的感觉,没关系,这个很正常。接下来,我结合一个具体的动态规划问题,来给你详细解释。
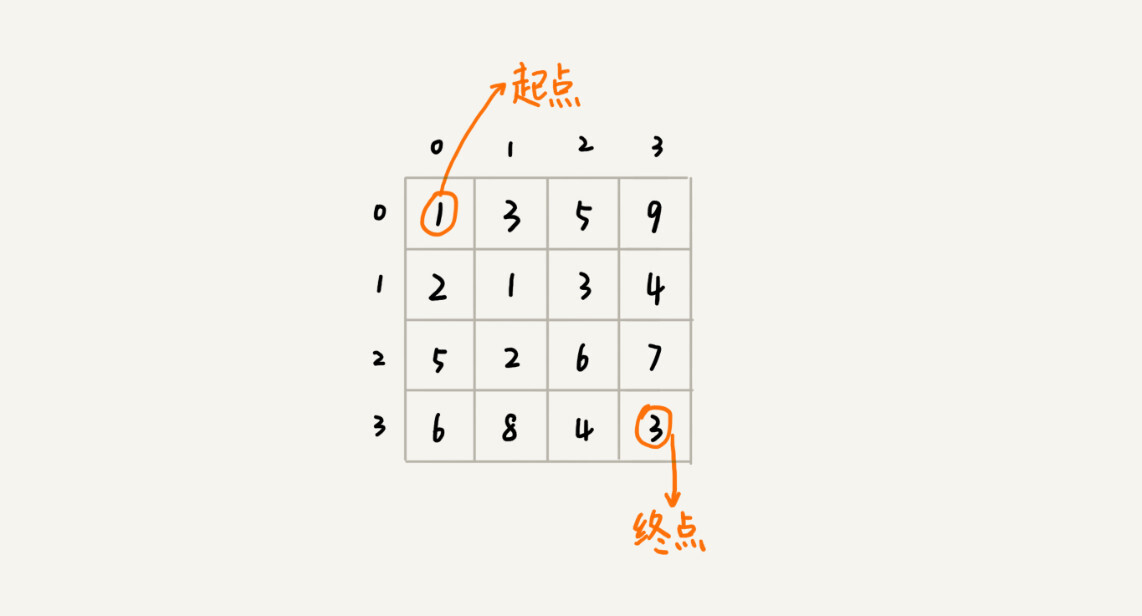
假设我们有一个 n 乘以 n 的矩阵 w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角,终止位置在右下角。我们将棋子从左上角移动到右下角。每次只能向右或者向下移动一位。从左上角到右下角,会有很多不同的路径可以走。我们把每条路径经过的数字加起来看作路径的长度。那从左上角移动到右下角的最短路径长度是多少呢?
我们先看看,这个问题是否符合“一个模型”?
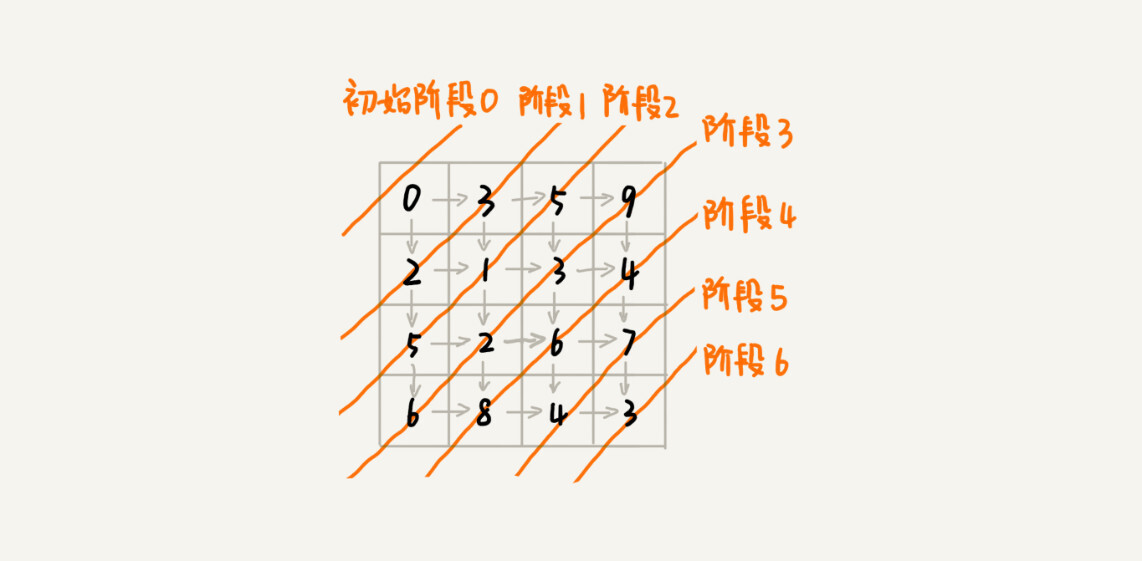
从 (0, 0) 走到 (n-1, n-1),总共要走 2*(n-1) 步,也就对应着 2*(n-1) 个阶段。每个阶段都有向右走或者向下走两种决策,并且每个阶段都会对应一个状态集合。
我们把状态定义为 min_dist(i, j),其中 i 表示行,j 表示列。min_dist 表达式的值表示从 (0, 0) 到达 (i, j) 的最短路径长度。所以,这个问题是一个多阶段决策最优解问题,符合动态规划的模型。
我们再来看,这个问题是否符合“三个特征”?
我们可以用回溯算法来解决这个问题。如果你自己写一下代码,画一下递归树,就会发现,递归树中有重复的节点。重复的节点表示,从左上角到节点对应的位置,有多种路线,这也能说明这个问题中存在重复子问题。
如果我们走到 (i, j) 这个位置,我们只能通过 (i-1, j),(i, j-1) 这两个位置移动过来,也就是说,我们想要计算 (i, j) 位置对应的状态,只需要关心 (i-1, j),(i, j-1) 两个位置对应的状态,并不关心棋子是通过什么样的路线到达这两个位置的。而且,我们仅仅允许往下和往右移动,不允许后退,所以,前面阶段的状态确定之后,不会被后面阶段的决策所改变,所以,这个问题符合“无后效性”这一特征。
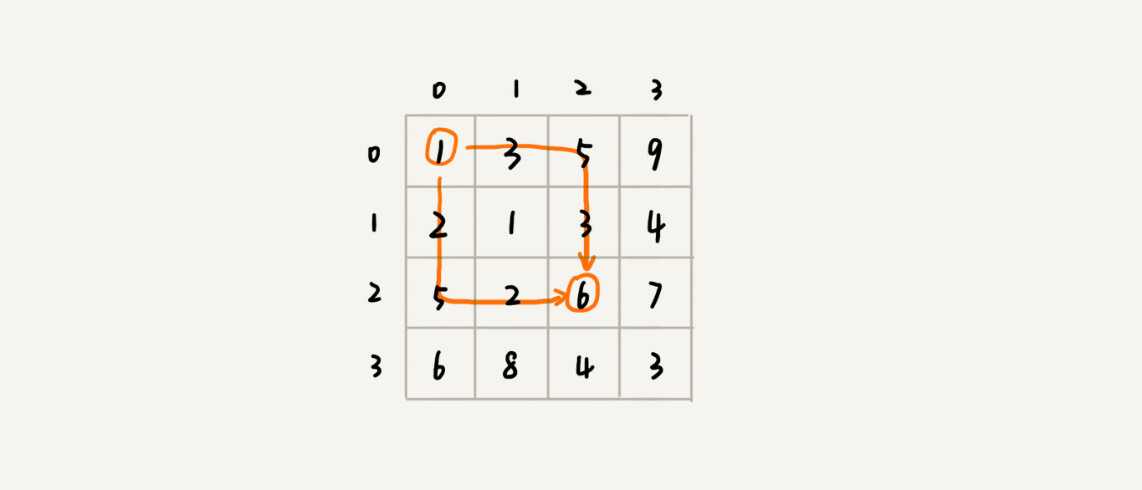
刚刚定义状态的时候,我们把从起始位置 (0, 0) 到 (i, j) 的最小路径,记作 min_dist(i, j)。因为我们只能往右或往下移动,所以,我们只有可能从 (i, j-1) 或者 (i-1, j) 两个位置到达 (i, j)。也就是说,到达 (i, j) 的最短路径要么经过 (i, j-1),要么经过 (i-1, j),而且到达 (i, j) 的最短路径肯定包含到达这两个位置的最短路径之一。换句话说就是,min_dist(i, j) 可以通过 min_dist(i, j-1) 和 min_dist(i-1, j) 两个状态推导出来。这就说明,这个问题符合“最优子结构”。
两种动态规划解题思路总结
刚刚我讲了,如何鉴别一个问题是否可以用动态规划来解决。现在,我再总结一下,动态规划解题的一般思路,让你面对动态规划问题的时候,能够有章可循,不至于束手无策。
我个人觉得,解决动态规划问题,一般有两种思路。我把它们分别叫作,状态转移表法和状态转移方程法。
1. 状态转移表法
一般能用动态规划解决的问题,都可以使用回溯算法的暴力搜索解决。所以,当我们拿到问题的时候,我们可以先用简单的回溯算法解决,然后定义状态,每个状态表示一个节点,然后对应画出递归树。从递归树中,我们很容易可以看出来,是否存在重复子问题,以及重复子问题是如何产生的。以此来寻找规律,看是否能用动态规划解决。
找到重复子问题之后,接下来,我们有两种处理思路,第一种是直接用回溯加“备忘录”的方法,来避免重复子问题。从执行效率上来讲,这跟动态规划的解决思路没有差别。第二种是使用动态规划的解决方法,状态转移表法。第一种思路,我就不讲了,你可以看看上一节的两个例子。我们重点来看状态转移表法是如何工作的。
我们先画出一个状态表。状态表一般都是二维的,所以你可以把它想象成二维数组。其中,每个状态包含三个变量,行、列、数组值。我们根据决策的先后过程,从前往后,根据递推关系,分阶段填充状态表中的每个状态。最后,我们将这个递推填表的过程,翻译成代码,就是动态规划代码了。
尽管大部分状态表都是二维的,但是如果问题的状态比较复杂,需要很多变量来表示,那对应的状态表可能就是高维的,比如三维、四维。那这个时候,我们就不适合用状态转移表法来解决了。一方面是因为高维状态转移表不好画图表示,另一方面是因为人脑确实很不擅长思考高维的东西。
现在,我们来看一下,如何套用这个状态转移表法,来解决之前那个矩阵最短路径的问题?
从起点到终点,我们有很多种不同的走法。我们可以穷举所有走法,然后对比找出一个最短走法。不过如何才能无重复又不遗漏地穷举出所有走法呢?我们可以用回溯算法这个比较有规律的穷举算法。
回溯算法的代码实现如下所示。代码很短,而且我前面也分析过很多回溯算法的例题,这里我就不多做解释了,你自己来看看。
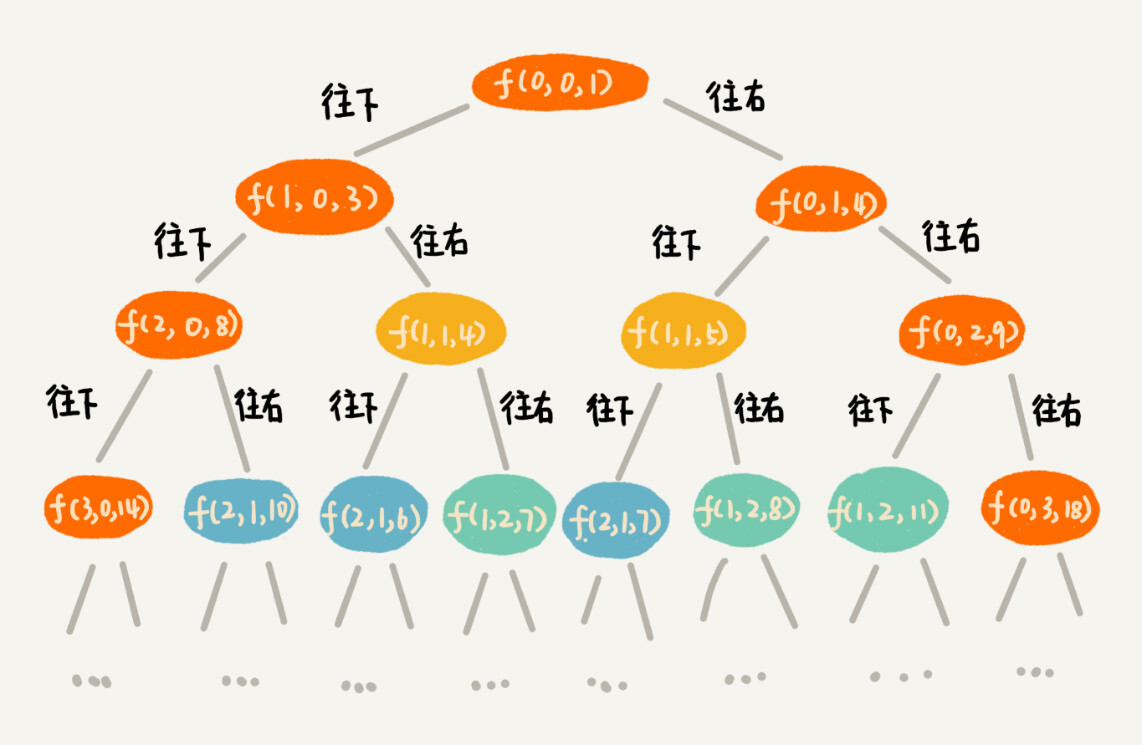
有了回溯代码之后,接下来,我们要画出递归树,以此来寻找重复子问题。在递归树中,一个状态(也就是一个节点)包含三个变量 (i, j, dist),其中 i,j 分别表示行和列,dist 表示从起点到达 (i, j) 的路径长度。从图中,我们看出,尽管 (i, j, dist) 不存在重复的,但是 (i, j) 重复的有很多。对于 (i, j) 重复的节点,我们只需要选择 dist 最小的节点,继续递归求解,其他节点就可以舍弃了。
既然存在重复子问题,我们就可以尝试看下,是否可以用动态规划来解决呢?
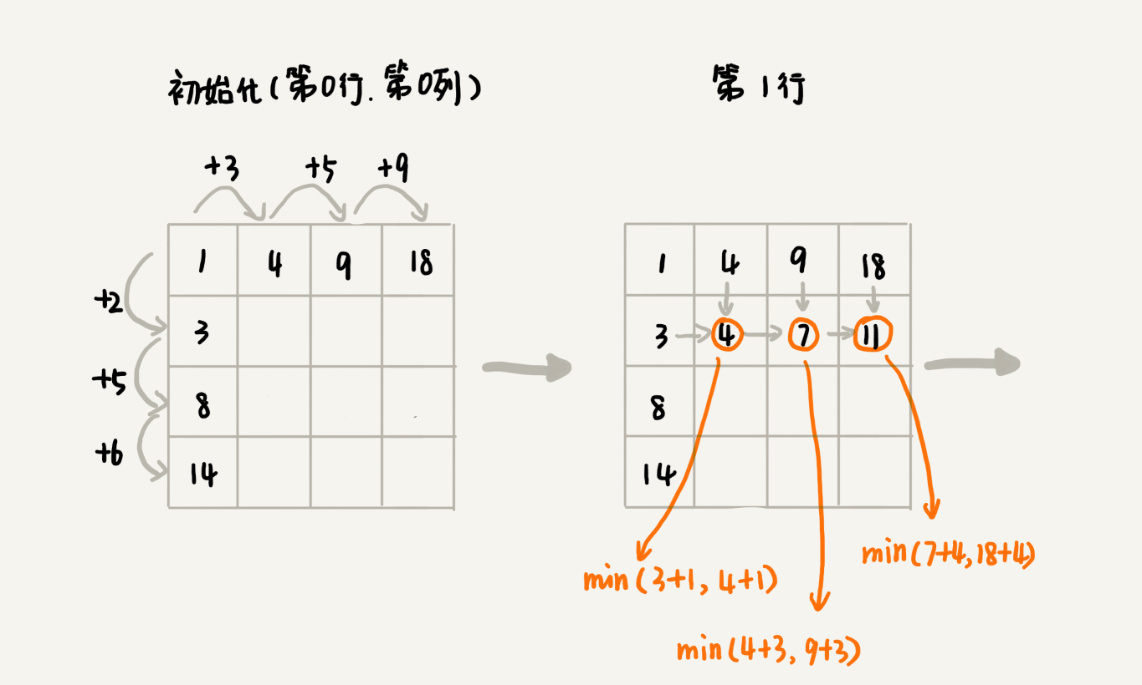
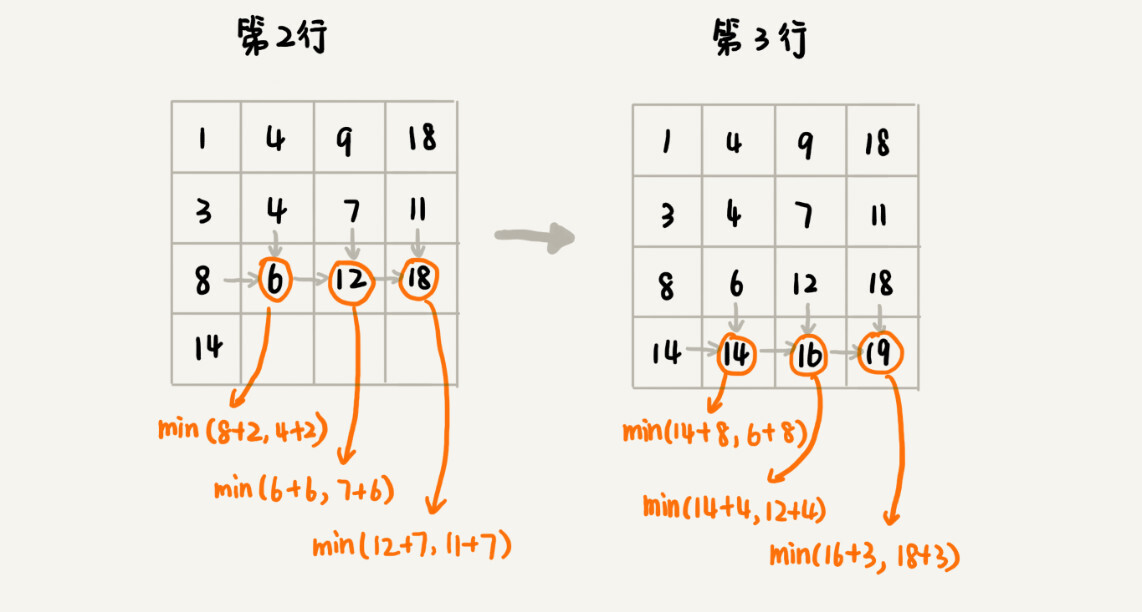
我们画出一个二维状态表,表中的行、列表示棋子所在的位置,表中的数值表示从起点到这个位置的最短路径。我们按照决策过程,通过不断状态递推演进,将状态表填好。为了方便代码实现,我们按行来进行依次填充。
弄懂了填表的过程,代码实现就简单多了。我们将上面的过程,翻译成代码,就是下面这个样子。结合着代码、图和文字描述,应该更容易理解我讲的内容。
2. 状态转移方程法
状态转移方程法有点类似递归的解题思路。我们需要分析,某个问题如何通过子问题来递归求解,也就是所谓的最优子结构。根据最优子结构,写出递归公式,也就是所谓的状态转移方程。有了状态转移方程,代码实现就非常简单了。一般情况下,我们有两种代码实现方法,一种是递归加“备忘录”,另一种是迭代递推。
我们还是拿刚才的例子来举例。最优子结构前面已经分析过了,你可以回过头去再看下。为了方便你查看,我把状态转移方程放到这里。
这里我强调一下,状态转移方程是解决动态规划的关键。如果我们能写出状态转移方程,那动态规划问题基本上就解决一大半了,而翻译成代码非常简单。但是很多动态规划问题的状态本身就不好定义,状态转移方程也就更不好想到。
下面我用递归加“备忘录”的方式,将状态转移方程翻译成来代码,你可以看看。对于另一种实现方式,跟状态转移表法的代码实现是一样的,只是思路不同。
两种动态规划解题思路到这里就讲完了。我要强调一点,不是每个问题都同时适合这两种解题思路。有的问题可能用第一种思路更清晰,而有的问题可能用第二种思路更清晰,所以,你要结合具体的题目来看,到底选择用哪种解题思路。
四种算法思想比较分析
到今天为止,我们已经学习了四种算法思想,贪心、分治、回溯和动态规划。今天的内容主要讲些理论知识,我正好一块儿也分析一下这四种算法,看看它们之间有什么区别和联系。
如果我们将这四种算法思想分一下类,那贪心、回溯、动态规划可以归为一类,而分治单独可以作为一类,因为它跟其他三个都不大一样。为什么这么说呢?前三个算法解决问题的模型,都可以抽象成我们今天讲的那个多阶段决策最优解模型,而分治算法解决的问题尽管大部分也是最优解问题,但是,大部分都不能抽象成多阶段决策模型。
回溯算法是个“万金油”。基本上能用的动态规划、贪心解决的问题,我们都可以用回溯算法解决。回溯算法相当于穷举搜索。穷举所有的情况,然后对比得到最优解。不过,回溯算法的时间复杂度非常高,是指数级别的,只能用来解决小规模数据的问题。对于大规模数据的问题,用回溯算法解决的执行效率就很低了。
尽管动态规划比回溯算法高效,但是,并不是所有问题,都可以用动态规划来解决。能用动态规划解决的问题,需要满足三个特征,最优子结构、无后效性和重复子问题。在重复子问题这一点上,动态规划和分治算法的区分非常明显。分治算法要求分割成的子问题,不能有重复子问题,而动态规划正好相反,动态规划之所以高效,就是因为回溯算法实现中存在大量的重复子问题。
贪心算法实际上是动态规划算法的一种特殊情况。它解决问题起来更加高效,代码实现也更加简洁。不过,它可以解决的问题也更加有限。它能解决的问题需要满足三个条件,最优子结构、无后效性和贪心选择性(这里我们不怎么强调重复子问题)。
其中,最优子结构、无后效性跟动态规划中的无异。“贪心选择性”的意思是,通过局部最优的选择,能产生全局的最优选择。每一个阶段,我们都选择当前看起来最优的决策,所有阶段的决策完成之后,最终由这些局部最优解构成全局最优解。
内容小结
今天的内容到此就讲完了,我带你来复习一下。
我首先讲了什么样的问题适合用动态规划解决。这些问题可以总结概括为“一个模型三个特征”。其中,“一个模型”指的是,问题可以抽象成分阶段决策最优解模型。“三个特征”指的是最优子节、无后效性和重复子问题。
然后,我讲了两种动态规划的解题思路。它们分别是状态转移表法和状态转移方程法。其中,状态转移表法解题思路大致可以概括为,回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 - 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码。状态转移方程法的大致思路可以概括为,找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码。
最后,我们对比了之前讲过的四种算法思想。贪心、回溯、动态规划可以解决的问题模型类似,都可以抽象成多阶段决策最优解模型。尽管分治算法也能解决最优问题,但是大部分问题的背景都不适合抽象成多阶段决策模型。
今天的内容比较偏理论,可能会不好理解。很多理论知识的学习,单纯的填鸭式讲给你听,实际上效果并不好。要想真的把这些理论知识理解透,化为己用,还是需要你自己多思考,多练习。等你做了足够多的题目之后,自然就能自己悟出一些东西,这样再回过头来看理论,就会非常容易看懂。
所以,在今天的内容中,如果有哪些地方你还不能理解,那也没关系,先放一放。下一节,我会运用今天讲到的理论,再解决几个动态规划的问题。等你学完下一节,可以再回过头来看下今天的理论知识,可能就会有一种顿悟的感觉。
课后思考
硬币找零问题,我们在贪心算法那一节中讲过一次。我们今天来看一个新的硬币找零问题。假设我们有几种不同币值的硬币 v1,v2,……,vn(单位是元)。如果我们要支付 w 元,求最少需要多少个硬币。比如,我们有 3 种不同的硬币,1 元、3 元、5 元,我们要支付 9 元,最少需要 3 个硬币(3 个 3 元的硬币)。
欢迎留言和我分享,也欢迎点击“请朋友读”,把今天的内容分享给你的好友,和他一起讨论、学习。
精选留言(51)
- yaya2019-01-03 48可以看做爬阶梯问题,分别可以走1.3.5步,怎么最少走到9步,动态转移方程为f(9)=1+min(f(8),f(6),f(4))
作者回复: 👍
- 郭霖2019-01-03 22动态规划状态转移表解法:
public int minCoins(int money) {
if (money == 1 || money == 3 || money == 5) return 1;
boolean [][] state = new boolean[money][money + 1];
if (money >= 1) state[0][1] = true;
if (money >= 3) state[0][3] = true;
if (money >= 5) state[0][5] = true;
for (int i = 1; i < money; i++) {
for (int j = 1; j <= money; j++) {
if (state[i - 1][j]) {
if (j + 1 <= money) state[i][j + 1] = true;
if (j + 3 <= money) state[i][j + 3] = true;
if (j + 5 <= money) state[i][j + 5] = true;
if (state[i][money]) return i + 1;
}
}
}
return money;
}展开 - 煦暖2019-01-03 9状态转移表法,二维状态表的图中,第一行下面的表达式:
文中“min(4+3, 8+3)”应该是“min(4+3, 9+3)”展开作者回复: 嗯嗯 是的 笔误 抱歉
- Alpha.2019-02-22 5回溯算法实现矩阵最短路径会有边界问题,下面是修改后的代码。
private static int MIN_DIS = Integer.MAX_VALUE;
public static void minDisByBT(int i, int j, int[][] w, int n, int distance) {
distance += w[i][j];
if (i == n - 1 && j == n - 1) {
if (distance < MIN_DIS) MIN_DIS = distance;
return;
}
if (i < n - 1) {
minDisByBT(i + 1, j, w, n, distance);
}
if (j < n - 1) {
minDisByBT(i, j + 1, w, n, distance);
}
}展开 - feifei2019-01-06 5经过一个星期的努力,这个动态规划终于有点感觉了,今天来做题,我也来试试解这个题目,在看了第一个童鞋的解法后,感觉这个写的太死了,再就是没有反推出哪些币的组合,我就自己来实现了下!
我也想说动态规划的解,真不容易啊,我按照老师提供的方法,先使用回塑写出了暴力搜索,然后再画出了递归树,找到状态组合,然后才来写这个动态规划,感觉好复杂,不过吧,这个使用状态转移方程,我感觉更难,比这个递归还难写。。。。。。,最主要是这个状态想不到,但这个动态规划代码写完了,我又感觉能写方程了,我想哭。。。。。。。
public int countMoneyMin(int[] moneyItems, int resultMemory) {
if (null == moneyItems || moneyItems.length < 1) {
return -1;
}
if (resultMemory < 1) {
return -1;
}
// 计算遍历的层数,此按最小金额来支付即为最大层数
int levelNum = resultMemory / moneyItems[0];
int leng = moneyItems.length;
int[][] status = new int[levelNum][resultMemory + 1];
// 初始化状态数组
for (int i = 0; i < levelNum; i++) {
for (int j = 0; j < resultMemory + 1; j++) {
status[i][j] = -1;
}
}
// 将第一层的数数据填充
for (int i = 0; i < leng; i++) {
status[0][moneyItems[i]] = moneyItems[i];
}
int minNum = -1;
// 计算推导状态
for (int i = 1; i < levelNum; i++) {
// 推导出当前状态
for (int j = 0; j < resultMemory; j++) {
if (status[i - 1][j] != -1) {
// 遍历元素,进行累加
for (int k = 0; k < leng; k++) {
if (j + moneyItems[k] <= resultMemory) {
status[i][j + moneyItems[k]] = moneyItems[k];
}
}
}
// 找到最小的张数
if (status[i][resultMemory] >= 0) {
minNum = i + 1;
break;
}
}
if (minNum > 0) {
break;
}
}
int befValue = resultMemory;
// 进行反推出,币的组合
for (int i = minNum - 1; i >= 0; i--) {
for (int j = resultMemory; j >= 0; j--) {
if (j == befValue) {
System.out.println("当前的为:" + status[i][j]);
befValue = befValue - status[i][j];
break;
}
}
}
return minNum;
}展开作者回复: 👍 都有这个似懂非懂的过程的 多练习 慢慢就有感觉了
- blacknhole2018-12-31 2状态转移方程法的代码实现有问题:
1,int minUp = Integer.MIN_VALUE;语句应赋值为Integer.MAX_VALUE。
2,返回前应将返回值赋值给mem[i][j]。作者回复: 已改 多谢指正
- 想当上帝的...2018-12-31 2放假了还在更新 赞展开
- 攻玉2019-03-12 1import numpy as np
老师 , 那个回溯法的代码好像不太对 , 我用 python 写了一个
import sys
minDist = sys.maxsize
n = 4 # 这是个 4*4 的矩阵 .
w = np.array([[0,3,5,9],[2,1,3,4],[5,2,6,7],[6,8,4,3]])
# dist = np.zeros((4,4)) # 定义 dist(i, j) 为到达点 (i,j) 的路径长度
# dist[i, j] = w[i,j] + min(dist[i-1, j] , dist[i, j-1])
def minDistBackTrace(i, j, dist, w, n):
global minDist
dist += w[i][j]
if i==n -1 and j == n-1 :
if dist < minDist: minDist = dist
return
if i < n-1:
minDistBackTrace(i + 1, j, dist, w, n)
if j < n-1:
minDistBackTrace(i , j + 1, dist, w, n)展开 - 菜菜2019-03-05 1老师,回溯法求矩阵最短路径的代码会出错,边界条件的问题
- Zix2019-02-26 1经测试,状态转移表法与状态转移方程法的代码均无误。
但是此问题最开始用的回溯法,会出现数组越界的问题,边界还需要再判断,请老师解答。 - Zix2019-02-26 1老师,回溯的那种解法,代码有问题,会出现数组越界,边界的问题。
作者回复: 嗯嗯 我再去看下
- 春去春又来2019-02-21 1老师,我按照文章里面的代码敲了一遍,
状态转移表法的那个代码运行结果等于 等于19
状态转移方程法的那个代码运行结果等于 18
不知道大家是不是这样的??????展开作者回复: 我擦,我研究下
- 猫头鹰爱拿...2019-01-08 1看了这一篇豁然开朗,上一篇的习题也会做了。感觉这些涉及多决策的习题基本上第一眼都能想到回溯法,但是用动态规划法就要好好想一想,关键还是老师说的动态转移方程式。我尝试用两种方法做了一遍,回溯法和动态规划法。
int minNum = Integer.MAX_VALUE;
/**
* 使用回溯法获取给定金额最小的硬币数量,调用时num为0
*
* @param coinVal
* 硬币值数组
* @param total
* 指定的金额
* @param num
* 每个解法所得到的硬币数量
*/
public void getLeastCoinNumByBackTracking(int[] coinVal, int total, int num) {
if (total == 0) {
if (num < minNum)
minNum = num;
return;
}
for (int i = 0; i < coinVal.length; i++) {
if (total - coinVal[i] >= 0) {
getLeastCoinNumByBackTracking(coinVal, total - coinVal[i],
num + 1);
}
}
}
/**
* 使用动态规划法获取给定金额下最小的硬币数量
*
* @param coinVal
* 硬币值数组
* @param total
* 给定金额
* @return 给定金额下最小的硬币数量
*/
public int getLeastCoinNumByDP(int[] coinVal, int total) {
// coinNum存放的是每个对应金额下最少硬币的最优解
int coinNum[] = new int[total + 1];
coinNum[0] = 0;
//初始化coinNum数组,硬币值数组对应的值的硬币数量都为1
for (int i = 0; i < coinVal.length; i++) {
coinNum[coinVal[i]] = 1;
}
for (int i = 1; i <= total; i++) {
if (coinNum[i] == 0) {
int minTemp = Integer.MAX_VALUE; // 获取每个i对应的最小硬币数值
for (int j = 0; j < coinVal.length; j++) {
if (i - coinVal[j] > 0) {
int v1 = coinNum[i - coinVal[j]] + 1;
if (v1 < minTemp) {
minTemp = v1;
}
}
}
coinNum[i] = minTemp;
}
}
return coinNum[total];
}展开 - Kudo2019-01-05 1思考题解答:
动态规划解法(python实现)
状态转移方程:min_count[i] = min(min_count[j] + 1) for any j < i
import sys
def minCoinCount(values, amount):
'''
values: 硬币面值数组
amount: 要凑的总价值
'''
min_count = [sys.maxsize] * (amount+1) # 初始化
min_count[0] = 0
for i in range(1, amount+1): # [1, amount+1)左闭右开
for j in range(i): # [0,i)左闭右开
for v in values: # 依次考察每种币值
if j + v == i and min_count[j] + 1 < min_count[i]: # 能凑齐且最小
min_count[i] = min_count[j] + 1
print(min_count[amount]) # 输出结果
# 使用方法
values = [1,3,5]
minCoinCount(values, 9)展开 - Kudo2019-01-04 1思考题解答
使用回溯法(python实现):
import sys
min_count = sys.maxsize # 用于追踪最小值
def minCoinCount(i, values, amount, ca):
'''
i: 硬币数量
values: 硬币面值数组
amount: 要凑的总价值
ca: current amount 当前价值
'''
global min_count
if ca == amount or i == amount: # 总共amount步
if ca == amount and i < min_count:
min_count = i
return
for v in values: # 依次考察每种币值
if ca + v <= amount: # 保证不超总值价
minCoinCount(i+1, values, amount, ca+v)
# 使用方法
values = [1,3,5]
minCoinCount(0, values, 9, 0)
print(min_count)展开 - farFlight2018-12-31 1用动态规划的方法,初始化那些等于币值的价值,然后从1开始一步一步推到w元,f(k)代表k元时最少的硬币数量,状态方程是:
f(k) = min(f(k-vi)) + 1, i需要遍历所有的币种。
另外,请问老师之后会多讲一些回溯的技巧吗?回溯方法虽然本身复杂度比较高,但是可以用一些剪枝技巧branch and bound,这样实际运行时间也能很快,而且很多复杂的问题用回溯法思路会比较简单。展开作者回复: 高级篇会讲到
- Monday2018-12-31 12018最后一次更新,我通读三遍跟上打卡了。本节理论归纳的很精简,适合动态规划求解的问题的特性:一个模型,三个特征。
一个模型:多阶段决策最优解
三个特征:最优子结构,无后效性,重复子问题。展开 - frogoscar2018-12-31 1动态规划的课太帅了。老师厉害展开
- Peng2019-05-13状态转移表法的回溯代码中有注释:// 调用方式:minDistBacktracing(0,0,0,w,n)
这样调用跟下面的递归树对不上吧,递归树的根节点是f(0,0,1)
能再明确一下吗展开作者回复: 是有点对不上哈。你可以独立的看。回溯代码只是为了解释重复子问题。
- 张高凯2019-04-24public static void main(String[] args) {
int[] money = {1, 3, 5};
int[] mem = new int[10];//下标表示当前的金额,值表示达到当前金额用的硬币数
for (int i = 0; i < 10; i++) {
mem[i] = -1;
}
for (int i = 0; i < money.length; i++) {//初始值设置,即选择一个硬币的情况
if (money[i] <= 9) {
mem[money[i]] = 1;
}
}
for (int j = 1; j <= 9; j++) {
if (mem[j] > 0)
for (int m = 0; m < money.length; m++) {
if (j + money[m] <= 9) { //金额不得超过9
if (mem[j + money[m]] == -1 || mem[j] + 1 < mem[j + money[m]])//关键判断:达到相同金额的情况,保留用硬币数目最小的
mem[j + money[m]] = mem[j] + 1;
}
}
}
System.out.println(mem[9]);
}展开