

下载APP



关闭

讲堂

客户端下载

兑换中心

企业版

渠道合作

推荐作者

23 | 二叉树基础（上）：什么样的二叉树适合用数组来存储？

2018-11-12 王争

数据结构与算法之美

进入课程



讲述：修阳

时长10:11大小4.67M



前面我们讲的都是线性表结构，栈、队列等等。今天我们讲一种非线性表结构，树。树这种数据结构比线性表的数据结构要复杂得多，内容也比较多，所以我会分四节来讲解。

我反复强调过，带着问题学习，是最有效的学习方式之一，所以在正式的内容开始之前，我还是给你出一道思考题：二叉树有哪几种存储方式？什么样的二叉树适合用数组来存储？

带着这些问题，我们就来学习今天的内容，树！

树（Tree）

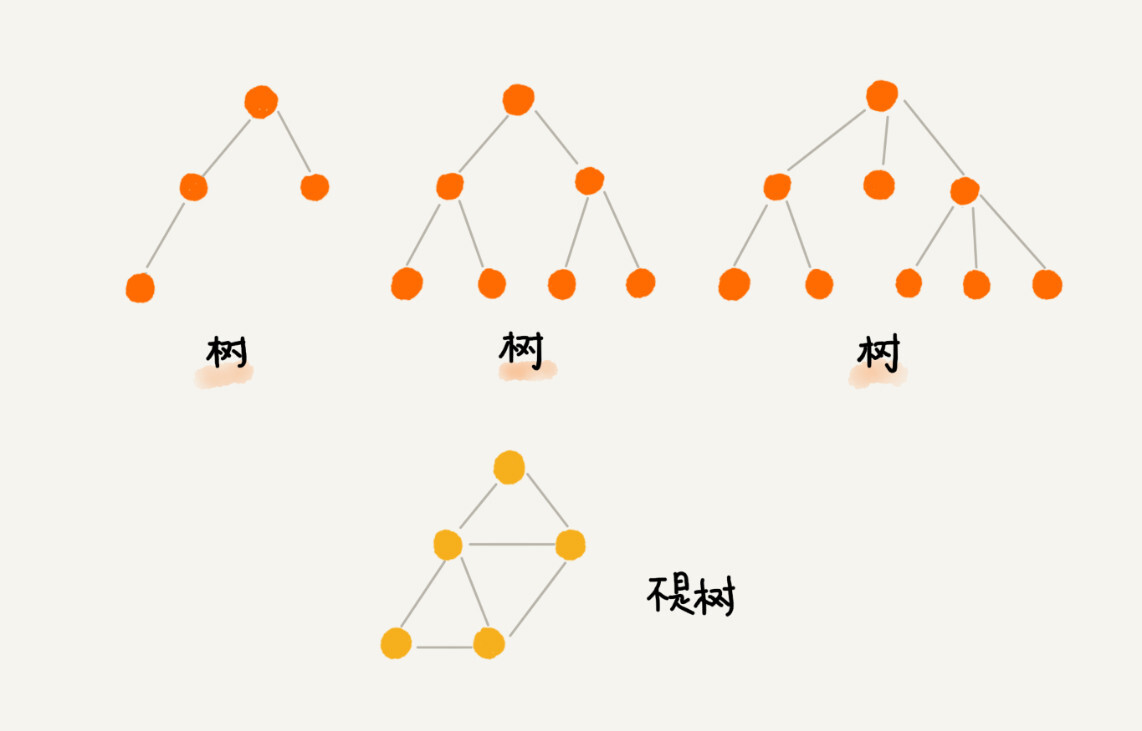
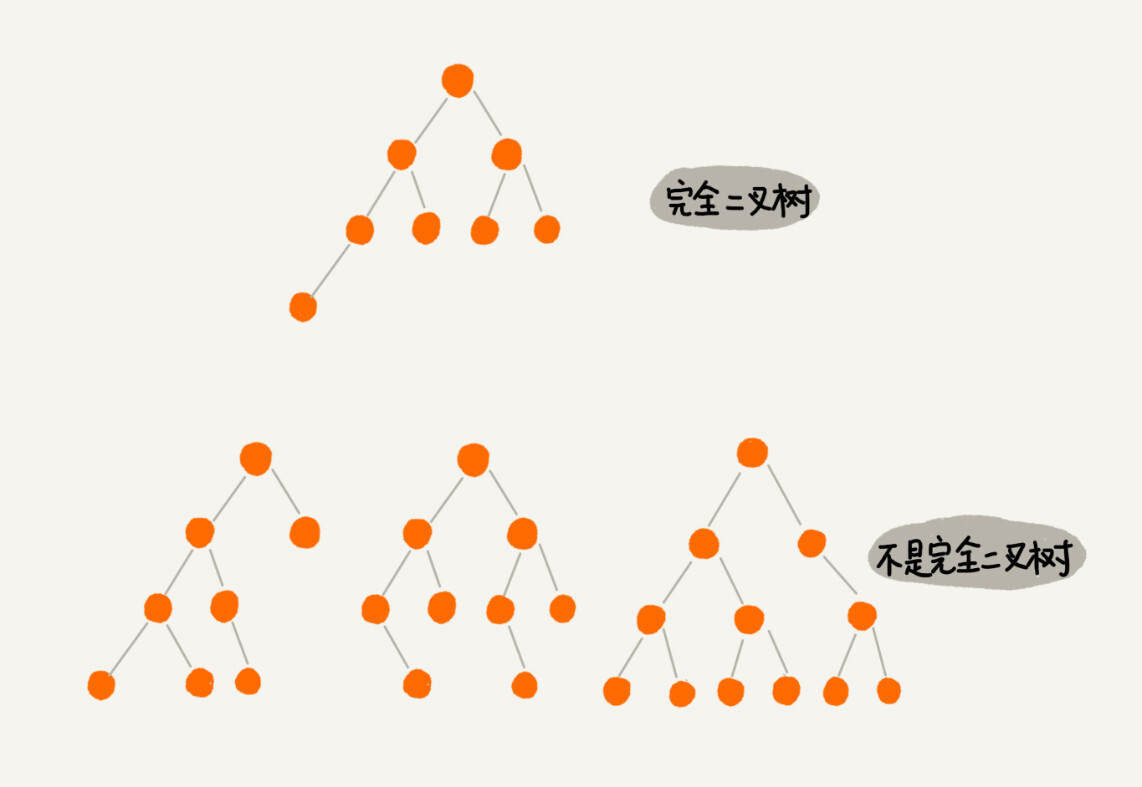
我们首先来看，什么是“树”？再完备的定义，都没有图直观。所以我在图中画了几棵“树”。你来看看，这些“树”都有什么特征？

你有没有发现，“树”这种数据结构真的很像我们现实生活中的“树”，这里面每个元素我们叫作“节点”；用来连线相邻节点之间的关系，我们叫作“父子关系”。

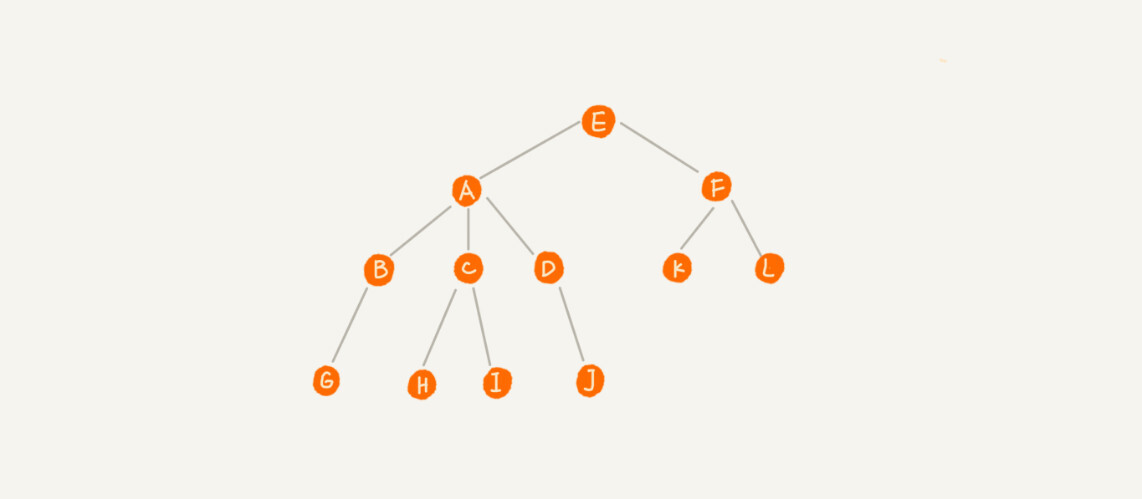
比如下面这幅图，A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫作根节点，也就是图中的节点 E。我们把没有子节点的节点叫作叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点。

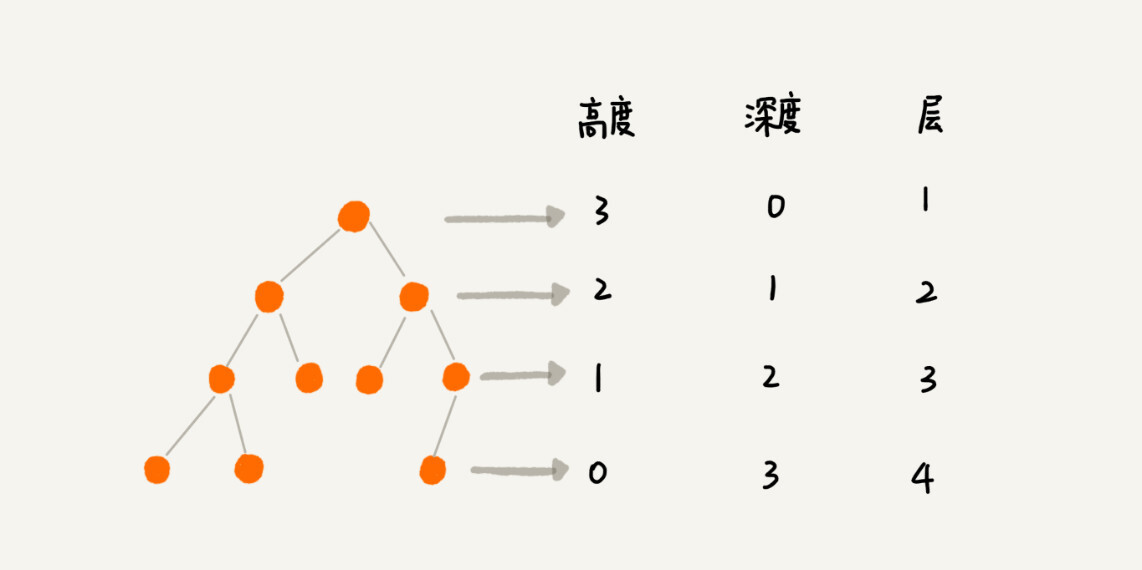
除此之外，关于“树”，还有三个比较相似的概念：高度（Height）、深度（Depth）、层（Level）。它们的定义是这样的：

这三个概念的定义比较容易混淆，描述起来也比较空洞。我举个例子说明一下，你一看应该就能明白。

记这几个概念，我还有一个小窍门，就是类比“高度”“深度”“层”这几个名词在生活中的含义。

在我们的生活中，“高度”这个概念，其实就是从下往上度量，比如我们要度量第 10 层楼的高度、第 13 层楼的高度，起点都是地面。所以，树这种数据结构的高度也是一样，从最底层开始计数，并且计数的起点是 0。

“深度”这个概念在生活中是从上往下度量的，比如水中鱼的深度，是从水平面开始度量的。所以，树这种数据结构的深度也是类似的，从根结点开始度量，并且计数起点也是 0。

“层数”跟深度的计算类似，不过，计数起点是 1，也就是说根节点的位于第 1 层。

二叉树（Binary Tree）

树结构多种多样，不过我们最常用还是二叉树。

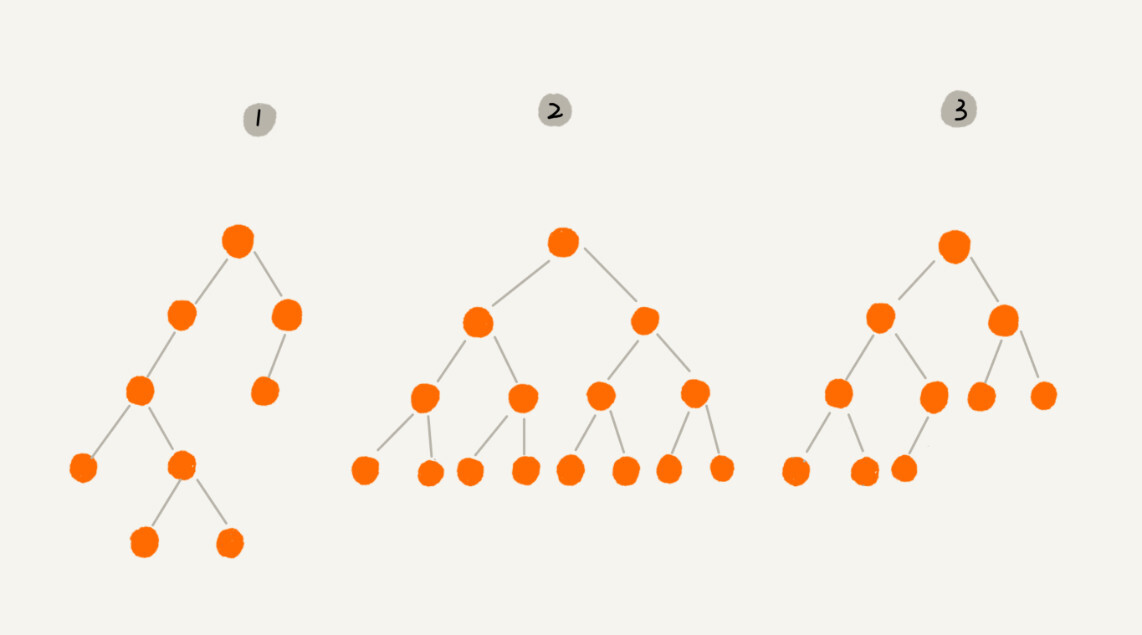
二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点。我画的这几个都是二叉树。以此类推，你可以想象一下四叉树、八叉树长什么样子。

这个图里面，有两个比较特殊的二叉树，分别是编号 2 和编号 3 这两个。

其中，编号 2 的二叉树中，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。

编号 3 的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。

满二叉树很好理解，也很好识别，但是完全二叉树，有的人可能就分不清了。我画了几个完全二叉树和非完全二叉树的例子，你可以对比着看看。

你可能会说，满二叉树的特征非常明显，我们把它单独拎出来讲，这个可以理解。但是完全二叉树的特征不怎么明显啊，单从长相上来看，完全二叉树并没有特别特殊的地方啊，更像是“芸芸众树”中的一种。

那我们为什么还要特意把它拎出来讲呢？为什么偏偏把最后一层的叶子节点靠左排列的叫完全二叉树？如果靠右排列就不能叫完全二叉树了吗？这个定义的由来或者说目的在哪里？

要理解完全二叉树定义的由来，我们需要先了解，如何表示（或者存储）一棵二叉树？

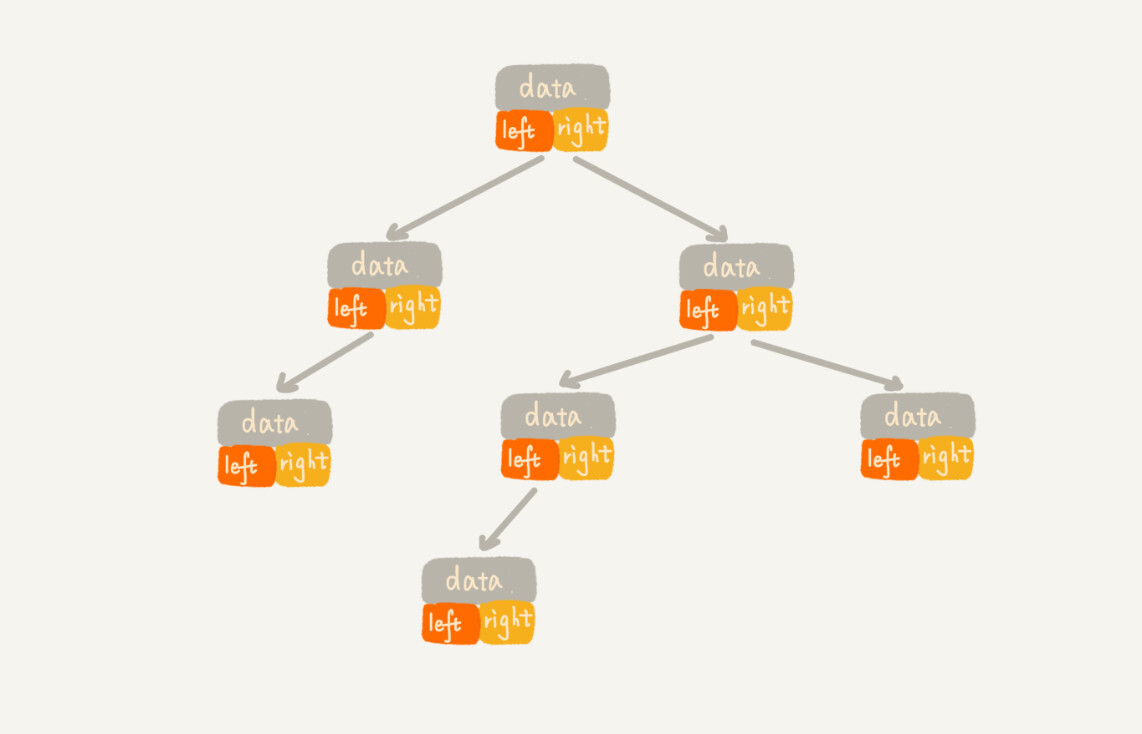
想要存储一棵二叉树，我们有两种方法，一种是基于指针或者引用的二叉链式存储法，一种是基于数组的顺序存储法。

我们先来看比较简单、直观的链式存储法。从图中你应该可以很清楚地看到，每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。这种存储方式我们比较常用。大部分二叉树代码都是通过这种结构来实现的。

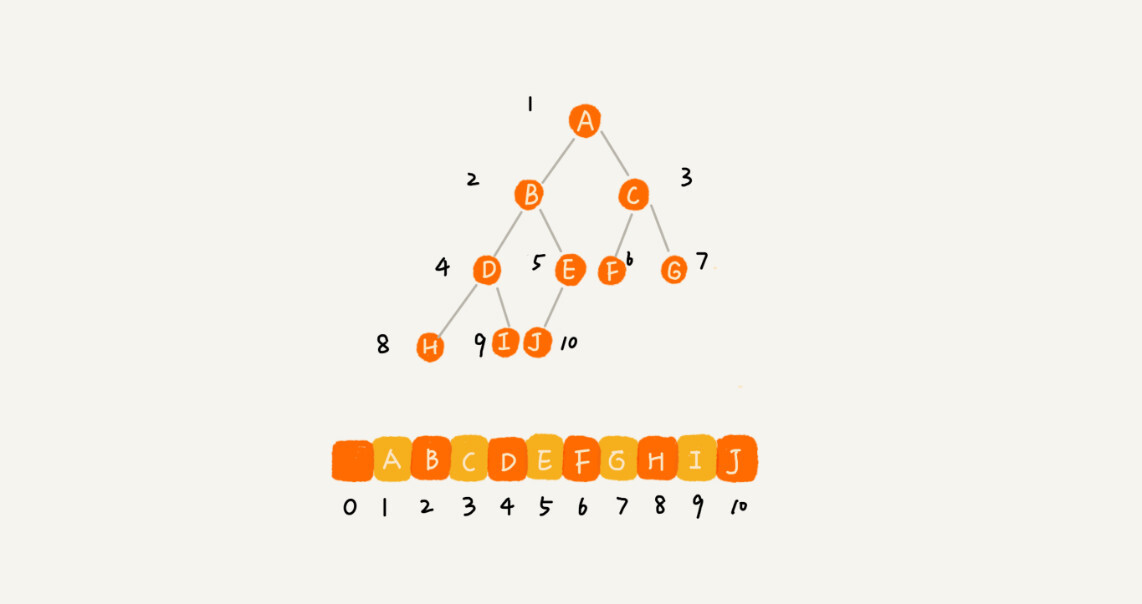
我们再来看，基于数组的顺序存储法。我们把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。以此类推，B 节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。

我来总结一下，如果节点 X 存储在数组中下标为 i 的位置，下标为 2 * i 的位置存储的就是左子节点，下标为 2 * i + 1 的位置存储的就是右子节点。反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。

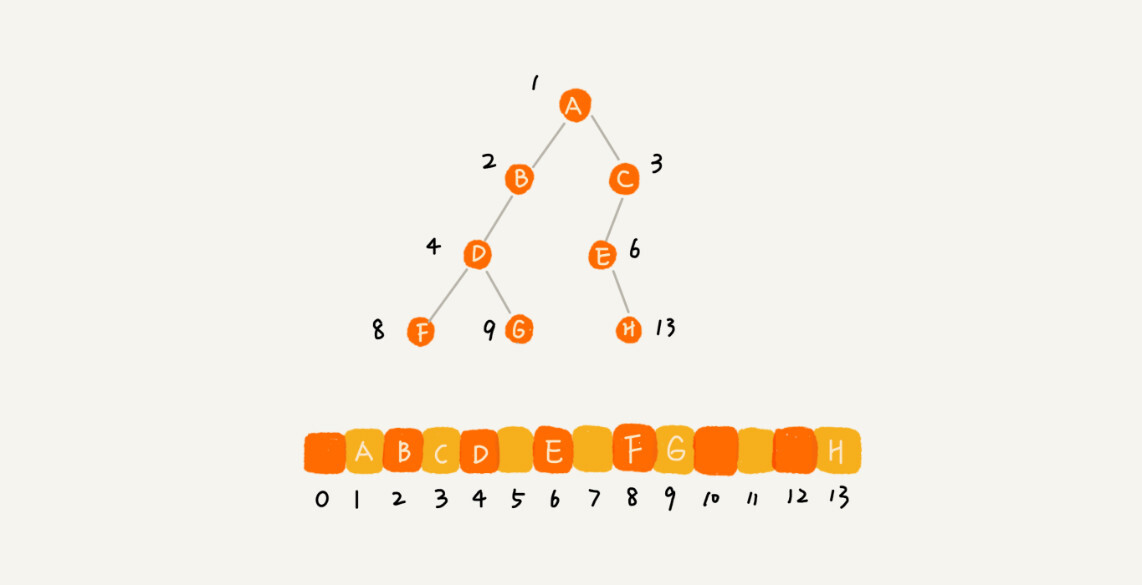
不过，我刚刚举的例子是一棵完全二叉树，所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树，其实会浪费比较多的数组存储空间。你可以看我举的下面这个例子。

所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因。

当我们讲到堆和堆排序的时候，你会发现，堆其实就是一种完全二叉树，最常用的存储方式就是数组。

二叉树的遍历

前面我讲了二叉树的基本定义和存储方法，现在我们来看二叉树中非常重要的操作，二叉树的遍历。这也是非常常见的面试题。

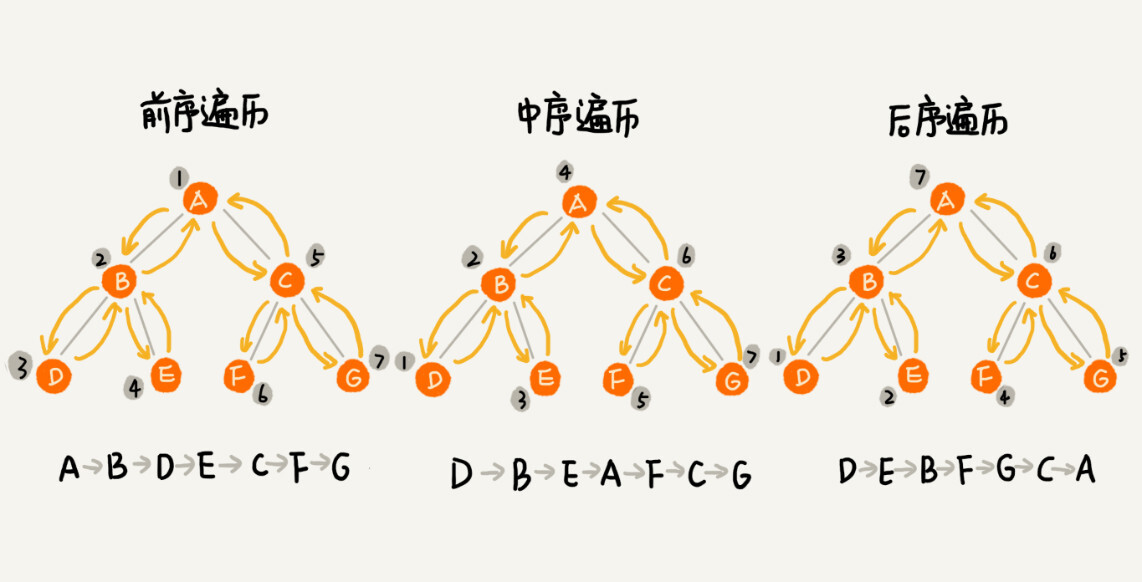
如何将所有节点都遍历打印出来呢？经典的方法有三种，前序遍历、中序遍历和后序遍历。其中，前、中、后序，表示的是节点与它的左右子树节点遍历打印的先后顺序。

前序遍历是指，对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
中序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它本身，最后打印它的右子树。
后序遍历是指，对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印这个节点本身。

实际上，二叉树的前、中、后序遍历就是一个递归的过程。比如，前序遍历，其实就是先打印根节点，然后再递归地打印左子树，最后递归地打印右子树。

写递归代码的关键，就是看能不能写出递推公式，而写递推公式的关键就是，如果要解决问题 A，就假设子问题 B、C 已经解决，然后再来看如何利用 B、C 来解决 A。所以，我们可以把前、中、后序遍历的递推公式都写出来。

 前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
 
中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
 
后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r复制代码

有了递推公式，代码写起来就简单多了。这三种遍历方式的代码，我都写出来了，你可以看看。

 void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印 root 节点
  preOrder(root->left);
  preOrder(root->right);
}
 
void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印 root 节点
  inOrder(root->right);
}
 
void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印 root 节点
}复制代码

二叉树的前、中、后序遍历的递归实现是不是很简单？你知道二叉树遍历的时间复杂度是多少吗？我们一起来看看。

从我前面画的前、中、后序遍历的顺序图，可以看出来，每个节点最多会被访问两次，所以遍历操作的时间复杂度，跟节点的个数 n 成正比，也就是说二叉树遍历的时间复杂度是 O(n)。

解答开篇 & 内容小结

今天，我讲了一种非线性表数据结构，树。关于树，有几个比较常用的概念你需要掌握，那就是：根节点、叶子节点、父节点、子节点、兄弟节点，还有节点的高度、深度、层数，以及树的高度。

我们平时最常用的树就是二叉树。二叉树的每个节点最多有两个子节点，分别是左子节点和右子节点。二叉树中，有两种比较特殊的树，分别是满二叉树和完全二叉树。满二叉树又是完全二叉树的一种特殊情况。

二叉树既可以用链式存储，也可以用数组顺序存储。数组顺序存储的方式比较适合完全二叉树，其他类型的二叉树用数组存储会比较浪费存储空间。除此之外，二叉树里非常重要的操作就是前、中、后序遍历操作，遍历的时间复杂度是 O(n)，你需要理解并能用递归代码来实现。

课后思考

给定一组数据，比如 1，3，5，6，9，10。你来算算，可以构建出多少种不同的二叉树？
我们讲了三种二叉树的遍历方式，前、中、后序。实际上，还有另外一种遍历方式，也就是按层遍历，你知道如何实现吗？

欢迎留言和我分享，我会第一时间给你反馈。

22 | 哈希算法（下）：哈希算法在分布式系统中有哪些应用？

24 | 二叉树基础（下）：有了如此高效的散列表，为什么还需要二叉树？

 写留言

精选留言(91)

失火的夏天

2018-11-12

 77

1.是卡特兰数，是C[n,2n] / (n+1)种形状，c是组合数，节点的不同又是一个全排列，一共就是n!*C[n,2n] / (n+1)个二叉树。可以通过数学归纳法推导得出。
2.层次遍历需要借助队列这样一个辅助数据结构。（其实也可以不用，这样就要自己手动去处理节点的关系，代码不太好理解，好处就是空间复杂度是o(1)。不过用队列比较好理解，缺点就是空间复杂度是o(n)）。根节点先入队列，然后队列不空，取出对头元素，如果左孩子存在就入列队，否则什么也不做，右孩子同理。直到队列为空，则表示树层次遍历结束。树的层次遍历，其实也是一个广度优先的遍历算法。

展开
meng

2018-11-18

 73

关于问题1，如果是完全二叉树，老师说过可以放在数组里面，那么问题是否可以简化为数组内的元素有多少种组合方式，这样的话，就是 n!，不知是否可以这样理解？

作者回复: 👍
姜威

2018-11-24

 23

树，总共包含4节内容。具体如下：
1.树、二叉树
2.二叉查找树
3.平衡二叉树、红黑树
4.递归树

一、树
1.树的常用概念
根节点、叶子节点、父节点、子节点、兄弟节点，还有节点的高度、深度以及层数，树的高度。
2.概念解释
节点：树中的每个元素称为节点
父子关系：相邻两节点的连线，称为父子关系
根节点：没有父节点的节点
叶子节点：没有子节点的节点
父节点：指向子节点的节点
子节点：被父节点指向的节点
兄弟节点：具有相同父节点的多个节点称为兄弟节点关系
节点的高度：节点到叶子节点的最长路径所包含的边数
节点的深度：根节点到节点的路径所包含的边数
节点的层数：节点的深度+1（根节点的层数是1）
树的高度：等于根节点的高度
二、二叉树
1.概念
①什么是二叉树？
每个节点最多只有2个子节点的树，这两个节点分别是左子节点和右子节点。
②什么是满二叉树？
有一种二叉树，除了叶子节点外，每个节点都有左右两个子节点，这种二叉树叫做满二叉树。
③什么是完全二叉树？
有一种二叉树，叶子节点都在最底下两层，最后一层叶子节都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫做完全二叉树。
2.完全二叉树的存储
①链式存储
每个节点由3个字段，其中一个存储数据，另外两个是指向左右子节点的指针。我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。这种存储方式比较常用，大部分二叉树代码都是通过这种方式实现的。
②顺序存储
用数组来存储，对于完全二叉树，如果节点X存储在数组中的下标为i，那么它的左子节点的存储下标为2*i，右子节点的下标为2*i+1，反过来，下标i/2位置存储的就是该节点的父节点。注意，根节点存储在下标为1的位置。完全二叉树用数组来存储时最省内存的方式。
3.二叉树的遍历
①前序遍历：对于树中的任意节点来说，先打印这个节点，然后再打印它的左子树，最后打印它的右子树。
②中序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它的本身，最后打印它的右子树。
③后序遍历：对于树中的任意节点来说，先打印它的左子树，然后再打印它的右子树，最后打印它本身。
前序遍历的递推公式：
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式：
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式：
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
时间复杂度：3种遍历方式中，每个节点最多会被访问2次，所以时间复杂度是O(n)。
三、思考
1.二叉树有哪几种存储方式？什么样的二叉树适合用数组来存储？
2.给定一组数据，比如1，3，5，6，9，10.你来算算，可以构建出多少种不同的二叉树？
3.我们讲了三种二叉树的遍历方式，前、中、后序。实际上，还有另一种遍历方式，也就是按层遍历，你知道如何实现吗？
4.如何用循环实现二叉树的遍历？

展开
言志

2018-11-21

 22

1、既然是数组了，说明是完全二叉树，应该有n的阶乘个组合。
2、二叉树按层遍历，可以看作以根结点为起点，图的广度优先遍历的问题。

作者回复: 👍
Jerry银银

2018-11-18

 17

第一题：
确定两点：
1）n个数，即n个节点，能构造出多少种不同形态的树？
2）n个数，有多少种不同的排列？
当确定以上两点，将【1)的结果】乘以【2)的结果】，即为最终的结果。
但是有一个注意的点：如果n中有相等的数，产生的总排列数就不是n！了哟

通过这一题，我学到了【卡塔兰数】：https://en.wikipedia.org/wiki/Catalan_number

第二题：
层序遍历，借用队列辅助即可，根节点先入队列，然后循环从队列中pop节点，将pop出来的节点的左子节点先入队列，右节点后入队列，依次循环，直到队列为空，遍历结束。

leetcode上有个类似的题目，链接为：https://leetcode.com/problems/binary-tree-level-order-traversal/
Java代码如下：
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        if (root == null) return new ArrayList<>(0);

        List<List<Integer>> result = new ArrayList<>();

        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);

        Queue<TreeNode> curLevelNodes = new LinkedList<TreeNode>();

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            curLevelNodes.offer(node);

            if (queue.isEmpty()) {
                List<Integer> list = new ArrayList<>(curLevelNodes.size());
                while (!curLevelNodes.isEmpty()) {
                    TreeNode curNode = curLevelNodes.poll();
                    list.add(curNode.val);

                    if (curNode.left != null) {
                        queue.offer(curNode.left);
                    }

                    if (curNode.right != null) {
                        queue.offer(curNode.right);
                    }

                }
                result.add(list);
            }
        }


        return result;
    }

}

展开
LeoBing

2018-11-17

 11

恕我愚钝。完全二叉树最后一层叶节点都靠左。可是图上节点9是靠右的，是不是我理解有什么问题，请教老师

展开
Laughing_L...

2018-11-30

 8

/**
     * 层次遍历二叉树
     *
     * @param root
     */
    public static void levelOrder(Node root) {
        if (root == null) {
            return;
        }
        LinkedList<Node> queue = new LinkedList<Node>();
        queue.add(root);
        while (!queue.isEmpty()) {
            Node currentNode = queue.poll();
            System.out.print(currentNode.getValue() + " ");
            if (currentNode.getLeft() != null) {
                queue.add(currentNode.getLeft());
            }
            if (currentNode.getRight() != null) {
                queue.add(currentNode.getRight());
            }
        }
    }

展开
明翼

2018-12-16

 7

我看很多人计算第一题都按照完全二叉树计算的，实际上并没有说完全二叉树，所以n阶乘肯定不对吧，只要是二叉树按照文中规则肯定可以按照数组存储，六个数字，前面五个数字最多浪费四个位置加上本身存储五个就是九个位置，然后六可以浪费一个，那就是一共十个位置，六个数字，有多少种放法就有多少种二叉树。

展开
Rephontil

2018-11-21

 6

现在评论的小伙伴少了好多，坚持学习的小伙伴是不是越来越少了？大家的热情呢？💪

作者回复: 有些人学得慢或者工作耽搁了。一直追着最新的看的不多
Liam

2018-11-12

 5

1 递归地理解一下：按住根节点，如果有k个左节点，则有n-k-1个右节点，分步乘法，f(n) = f(k) * f(n - k - 1) ，k可能性从0 到 n - 1 ,分步加法： f(n) = f(0)f(n-1) + ... + f(n-1)f(0) ，怎么计算该递推公式呢？参考Catalon数

展开
天二

2019-01-21

 4

老师你在计算便利二叉树时间复杂度的时候说，“从我前面画的前、中、后序遍历的顺序图，可以看出来，每个节点最多会被访问两次”，我想知道都是哪两次呢？可否帮忙解惑，从图中没看出来

作者回复: 第一次遍历到的时候算一次。递归返回的时候再一次。不过，这些说法都很笼统，你只要知道每个节点都被访问了一次，并且被访问的次数是常数次就可以了。
涂

2019-03-15

 3

前、中、后序遍历，主要是针对父节点的打印顺序。父左右为前序，左父右为中序，左右父为后序
kakasi

2018-11-26

 3

思考题：
1. 一组数能构建多少个二叉树？
第一时间想到只要排列位置有改变，那么就应该是新的二叉树。组合排列的公式有点忘记了。。。那么用笨方法：
当只有1个数的时候，能构建1个二叉树；2个数时是2个二叉树；3个数有6个二叉树；再看下4个数，原来是24个；最后得出n!
2. 层序遍历二叉树：
数组和链表的方式都一样。先打印本身的数据，然后将左右节点塞到一个队列中；从队列里取第一个节点打印数据，并将其左右节点再塞到队列，以此类推。

展开
传说中的成...

2018-11-12

 3

刚刚思考了完全二叉树的定义叶子结点必须要在最后两层如果不在最后两层的话通过数组顺序存储也会浪费空间吧

展开

作者回复: 是的
D→_→M

2018-11-12

 3

老师是否可以在您专栏的github上传一下二叉树这几节的相关代码，还有除了递归遍历二叉树，循环遍历是否也可以讲一下，或者在github上上传一下相关代码，自行研究学习。

作者回复: 非递归遍历比较复杂不建议非得给自己制造学习难度除非是为了面试。其他的二叉树的代码我会放到github上
nothing

2018-11-12

 3

后序遍历节点不是最多被访问三次嘛，还有那个深度我们学的深度和层次是一样的哇

作者回复: 1 从图上看是两次
2 从生活中的理解来说应该没有第0层之说但是有深度为0的说法
往事随风，...

2018-11-12

 3

按照蹭便利使用队列，广度优先搜索

展开
🔥

2018-11-20

 2

老师我想问一下，数组存储的时候跟节点为啥是在下标为1的位置而不是0
Alex

2019-04-28

 1

我看评论有人误解文章所说的完全二叉树--“最后一层的叶子节点都靠左排列。”然而图例中 I 节点明明是右节点，怎么就被称作完全二叉树？其实刚开始我也理解错了。这里说的 “最后一层的叶子节点都靠左排列”不是最后一层的子节点是左节点，而是指最后一层的子节点，从左数到右是连续，中间没有断开，缺少节点（如图例H、I、J是连续的）。结合下文所说的基于数组的顺序存储法，可以知道完全二叉树是不会浪费内存的。其实简单理解，完全是为了省内存而提出这样的概念

展开
极明

2019-02-05

 1

感谢老师让我明白了为什么需要完全二叉树

展开

	前序遍历的递推公式：
	preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)

	中序遍历的递推公式：
	inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)

	后序遍历的递推公式：
	postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

	void preOrder(Node* root) {
	if (root == null) return;
	print root // 此处为伪代码，表示打印 root 节点
	preOrder(root->left);
	preOrder(root->right);
	}

	void inOrder(Node* root) {
	if (root == null) return;
	inOrder(root->left);
	print root // 此处为伪代码，表示打印 root 节点
	inOrder(root->right);
	}

	void postOrder(Node* root) {
	if (root == null) return;
	postOrder(root->left);
	postOrder(root->right);
	print root // 此处为伪代码，表示打印 root 节点
	}