16 | 二分查找(下):如何快速定位IP对应的省份地址?

讲述:修阳
时长11:47大小5.40M
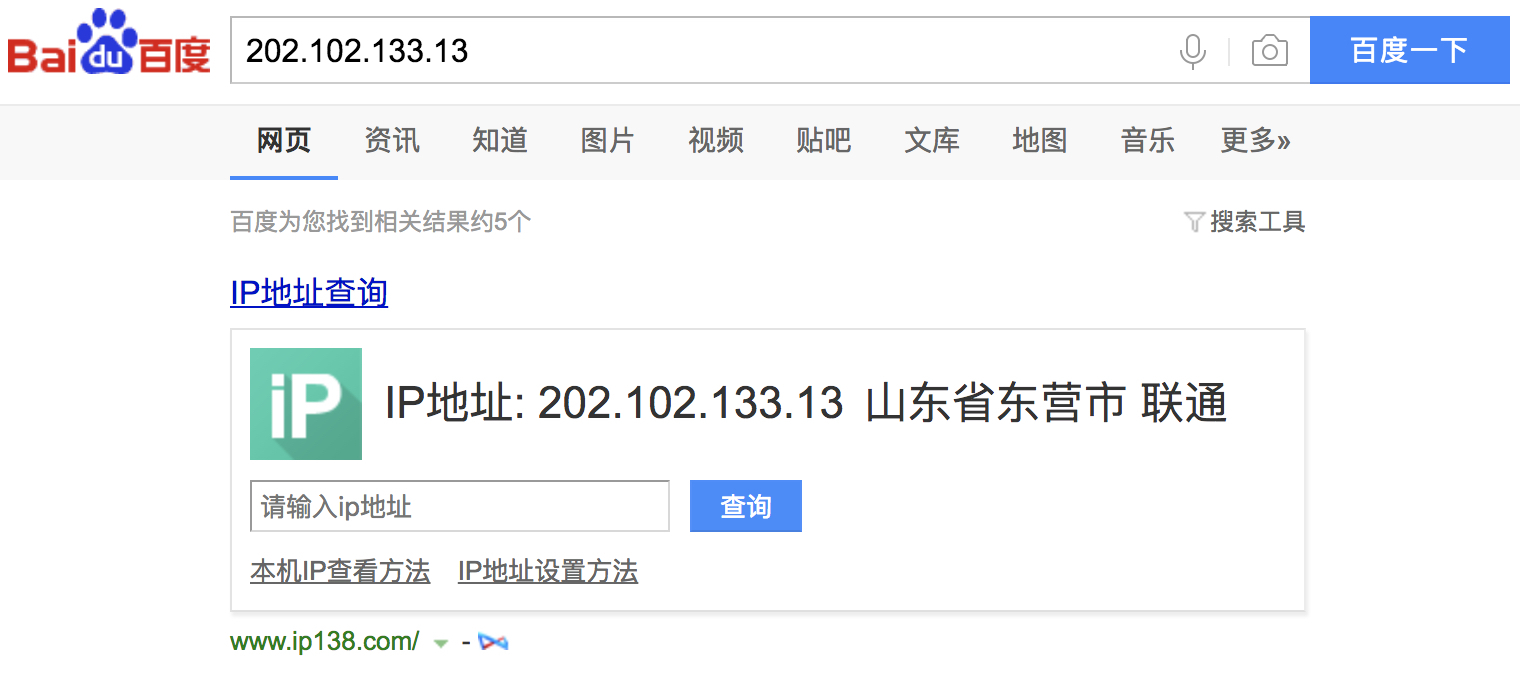
通过 IP 地址来查找 IP 归属地的功能,不知道你有没有用过?没用过也没关系,你现在可以打开百度,在搜索框里随便输一个 IP 地址,就会看到它的归属地。
这个功能并不复杂,它是通过维护一个很大的 IP 地址库来实现的。地址库中包括 IP 地址范围和归属地的对应关系。
当我们想要查询 202.102.133.13 这个 IP 地址的归属地时,我们就在地址库中搜索,发现这个 IP 地址落在 [202.102.133.0, 202.102.133.255] 这个地址范围内,那我们就可以将这个 IP 地址范围对应的归属地“山东东营市”显示给用户了。
现在我的问题是,在庞大的地址库中逐一比对 IP 地址所在的区间,是非常耗时的。假设我们有 12 万条这样的 IP 区间与归属地的对应关系,如何快速定位出一个 IP 地址的归属地呢?
是不是觉得比较难?不要紧,等学完今天的内容,你就会发现这个问题其实很简单。
上一节我讲了二分查找的原理,并且介绍了最简单的一种二分查找的代码实现。今天我们来讲几种二分查找的变形问题。
不知道你有没有听过这样一个说法:“十个二分九个错”。二分查找虽然原理极其简单,但是想要写出没有 Bug 的二分查找并不容易。
唐纳德·克努特(Donald E.Knuth)在《计算机程序设计艺术》的第 3 卷《排序和查找》中说到:“尽管第一个二分查找算法于 1946 年出现,然而第一个完全正确的二分查找算法实现直到 1962 年才出现。”
你可能会说,我们上一节学的二分查找的代码实现并不难写啊。那是因为上一节讲的只是二分查找中最简单的一种情况,在不存在重复元素的有序数组中,查找值等于给定值的元素。最简单的二分查找写起来确实不难,但是,二分查找的变形问题就没那么好写了。
二分查找的变形问题很多,我只选择几个典型的来讲解,其他的你可以借助我今天讲的思路自己来分析。
需要特别说明一点,为了简化讲解,今天的内容,我都以数据是从小到大排列为前提,如果你要处理的数据是从大到小排列的,解决思路也是一样的。同时,我希望你最好先自己动手试着写一下这 4 个变形问题,然后再看我的讲述,这样你就会对我说的“二分查找比较难写”有更加深的体会了。
变体一:查找第一个值等于给定值的元素
上一节中的二分查找是最简单的一种,即有序数据集合中不存在重复的数据,我们在其中查找值等于某个给定值的数据。如果我们将这个问题稍微修改下,有序数据集合中存在重复的数据,我们希望找到第一个值等于给定值的数据,这样之前的二分查找代码还能继续工作吗?
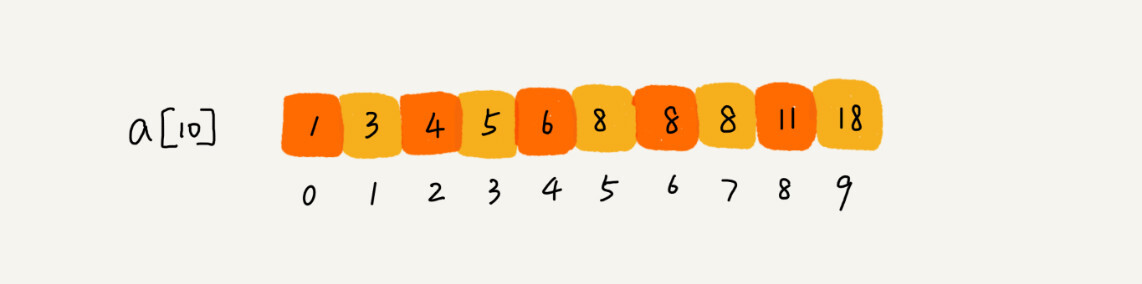
比如下面这样一个有序数组,其中,a[5],a[6],a[7] 的值都等于 8,是重复的数据。我们希望查找第一个等于 8 的数据,也就是下标是 5 的元素。
如果我们用上一节课讲的二分查找的代码实现,首先拿 8 与区间的中间值 a[4] 比较,8 比 6 大,于是在下标 5 到 9 之间继续查找。下标 5 和 9 的中间位置是下标 7,a[7] 正好等于 8,所以代码就返回了。
尽管 a[7] 也等于 8,但它并不是我们想要找的第一个等于 8 的元素,因为第一个值等于 8 的元素是数组下标为 5 的元素。我们上一节讲的二分查找代码就无法处理这种情况了。所以,针对这个变形问题,我们可以稍微改造一下上一节的代码。
100 个人写二分查找就会有 100 种写法。网上有很多关于变形二分查找的实现方法,有很多写得非常简洁,比如下面这个写法。但是,尽管简洁,理解起来却非常烧脑,也很容易写错。
看完这个实现之后,你是不是觉得很不好理解?如果你只是死记硬背这个写法,我敢保证,过不了几天,你就会全都忘光,再让你写,90% 的可能会写错。所以,我换了一种实现方法,你看看是不是更容易理解呢?
我来稍微解释一下这段代码。a[mid] 跟要查找的 value 的大小关系有三种情况:大于、小于、等于。对于 a[mid]>value 的情况,我们需要更新 high= mid-1;对于 a[mid]<value 的情况,我们需要更新 low=mid+1。这两点都很好理解。那当 a[mid]=value 的时候应该如何处理呢?
如果我们查找的是任意一个值等于给定值的元素,当 a[mid] 等于要查找的值时,a[mid] 就是我们要找的元素。但是,如果我们求解的是第一个值等于给定值的元素,当 a[mid] 等于要查找的值时,我们就需要确认一下这个 a[mid] 是不是第一个值等于给定值的元素。
我们重点看第 11 行代码。如果 mid 等于 0,那这个元素已经是数组的第一个元素,那它肯定是我们要找的;如果 mid 不等于 0,但 a[mid] 的前一个元素 a[mid-1] 不等于 value,那也说明 a[mid] 就是我们要找的第一个值等于给定值的元素。
如果经过检查之后发现 a[mid] 前面的一个元素 a[mid-1] 也等于 value,那说明此时的 a[mid] 肯定不是我们要查找的第一个值等于给定值的元素。那我们就更新 high=mid-1,因为要找的元素肯定出现在 [low, mid-1] 之间。
对比上面的两段代码,是不是下面那种更好理解?实际上,很多人都觉得变形的二分查找很难写,主要原因是太追求第一种那样完美、简洁的写法。而对于我们做工程开发的人来说,代码易读懂、没 Bug,其实更重要,所以我觉得第二种写法更好。
变体二:查找最后一个值等于给定值的元素
前面的问题是查找第一个值等于给定值的元素,我现在把问题稍微改一下,查找最后一个值等于给定值的元素,又该如何做呢?
如果你掌握了前面的写法,那这个问题你应该很轻松就能解决。你可以先试着实现一下,然后跟我写的对比一下。
我们还是重点看第 11 行代码。如果 a[mid] 这个元素已经是数组中的最后一个元素了,那它肯定是我们要找的;如果 a[mid] 的后一个元素 a[mid+1] 不等于 value,那也说明 a[mid] 就是我们要找的最后一个值等于给定值的元素。
如果我们经过检查之后,发现 a[mid] 后面的一个元素 a[mid+1] 也等于 value,那说明当前的这个 a[mid] 并不是最后一个值等于给定值的元素。我们就更新 low=mid+1,因为要找的元素肯定出现在 [mid+1, high] 之间。
变体三:查找第一个大于等于给定值的元素
现在我们再来看另外一类变形问题。在有序数组中,查找第一个大于等于给定值的元素。比如,数组中存储的这样一个序列:3,4,6,7,10。如果查找第一个大于等于 5 的元素,那就是 6。
实际上,实现的思路跟前面的那两种变形问题的实现思路类似,代码写起来甚至更简洁。
如果 a[mid] 小于要查找的值 value,那要查找的值肯定在 [mid+1, high] 之间,所以,我们更新 low=mid+1。
对于 a[mid] 大于等于给定值 value 的情况,我们要先看下这个 a[mid] 是不是我们要找的第一个值大于等于给定值的元素。如果 a[mid] 前面已经没有元素,或者前面一个元素小于要查找的值 value,那 a[mid] 就是我们要找的元素。这段逻辑对应的代码是第 7 行。
如果 a[mid-1] 也大于等于要查找的值 value,那说明要查找的元素在 [low, mid-1] 之间,所以,我们将 high 更新为 mid-1。
变体四:查找最后一个小于等于给定值的元素
现在,我们来看最后一种二分查找的变形问题,查找最后一个小于等于给定值的元素。比如,数组中存储了这样一组数据:3,5,6,8,9,10。最后一个小于等于 7 的元素就是 6。是不是有点类似上面那一种?实际上,实现思路也是一样的。
有了前面的基础,你完全可以自己写出来了,所以我就不详细分析了。我把代码贴出来,你可以写完之后对比一下。
解答开篇
好了,现在我们回头来看开篇的问题:如何快速定位出一个 IP 地址的归属地?
现在这个问题应该很简单了。如果 IP 区间与归属地的对应关系不经常更新,我们可以先预处理这 12 万条数据,让其按照起始 IP 从小到大排序。如何来排序呢?我们知道,IP 地址可以转化为 32 位的整型数。所以,我们可以将起始地址,按照对应的整型值的大小关系,从小到大进行排序。
然后,这个问题就可以转化为我刚讲的第四种变形问题“在有序数组中,查找最后一个小于等于某个给定值的元素”了。
当我们要查询某个 IP 归属地时,我们可以先通过二分查找,找到最后一个起始 IP 小于等于这个 IP 的 IP 区间,然后,检查这个 IP 是否在这个 IP 区间内,如果在,我们就取出对应的归属地显示;如果不在,就返回未查找到。
内容小结
上一节我说过,凡是用二分查找能解决的,绝大部分我们更倾向于用散列表或者二叉查找树。即便是二分查找在内存使用上更节省,但是毕竟内存如此紧缺的情况并不多。那二分查找真的没什么用处了吗?
实际上,上一节讲的求“值等于给定值”的二分查找确实不怎么会被用到,二分查找更适合用在“近似”查找问题,在这类问题上,二分查找的优势更加明显。比如今天讲的这几种变体问题,用其他数据结构,比如散列表、二叉树,就比较难实现了。
变体的二分查找算法写起来非常烧脑,很容易因为细节处理不好而产生 Bug,这些容易出错的细节有:终止条件、区间上下界更新方法、返回值选择。所以今天的内容你最好能用自己实现一遍,对锻炼编码能力、逻辑思维、写出 Bug free 代码,会很有帮助。
课后思考
我们今天讲的都是非常规的二分查找问题,今天的思考题也是一个非常规的二分查找问题。如果有序数组是一个循环有序数组,比如 4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法呢?
欢迎留言和我分享,我会第一时间给你反馈。
精选留言(103)
- Smallfly 置顶2018-10-27 134有三种方法查找循环有序数组
一、
1. 找到分界下标,分成两个有序数组
2. 判断目标值在哪个有序数据范围内,做二分查找
二、
1. 找到最大值的下标 x;
2. 所有元素下标 +x 偏移,超过数组范围值的取模;
3. 利用偏移后的下标做二分查找;
4. 如果找到目标下标,再作 -x 偏移,就是目标值实际下标。
两种情况最高时耗都在查找分界点上,所以时间复杂度是 O(N)。
复杂度有点高,能否优化呢?
三、
我们发现循环数组存在一个性质:以数组中间点为分区,会将数组分成一个有序数组和一个循环有序数组。
如果首元素小于 mid,说明前半部分是有序的,后半部分是循环有序数组;
如果首元素大于 mid,说明后半部分是有序的,前半部分是循环有序的数组;
如果目标元素在有序数组范围中,使用二分查找;
如果目标元素在循环有序数组中,设定数组边界后,使用以上方法继续查找。
时间复杂度为 O(logN)。展开 - zixuan2018-10-31 42思考题对应leetcode 33题,大家可以去练习展开
- Victor2018-10-27 9今天的IP地址归属地问题,从工程实现的角度考虑,我更偏向于直接使用关系型数据库实现。
也就是将12w条归属地与IP区间的开始、结束存入数据库中。
数据库表ip_table有如下字段:area_name | start_ip | end_ip ,start_ip及end_ip 均建立索引
SQL语句:
select area_name from ip_table where input_ip >= start_ip and input_ip <= end_ip;
学习算法的课程常常和自己工程开发的实际结合在一起,感觉两者是相互促进理解的过程。展开作者回复: 数据库可以 单性能会受限
- 王艳红2019-03-05 8王老师,有一个疑惑不太明白
int mid = low + ((high - low)>>1)
这句,为什么要用这种写法呢?我看之前的简单的额二分查找是
int mid = (low + high)/2展开作者回复: 下面的写法有可能会导致溢出,比如low很大,high也很大,之和就溢出了。
- charon2018-10-26 8用JavaScript实现的最基本的思考题:
array是传入的数组,value是要查找的值
思路是通过对比low,high的值来判断value所在的区间,不用多循环一遍找偏移量了~
function search(array,value){
let low = 0;
let high = array.length - 1;
while(low <= high){
let mid = low + ((high - low) >> 1);
if(value == array[low]) return low;
if(value == array[high]) return high;
if(value == array[mid]) return mid;
if(value > array[mid] && value > array[high] && array[mid] < array[low]){
high = mid - 1;
}else if(value < array[mid] && value < array[low] && array[mid] < array[low]){
high = mid - 1;
}else if(value < array[mid] && value > array[low]){
high = mid - 1;
}else{
low = mid + 1;
}
}
return -1
}展开 - 舍得2018-10-27 6第一段代码有漏洞,且不说int能不能表示数组的下标问题,毕竟这个数组能越界说明相当庞大了;
主要问题在于,如果我给定的数大于任何一个数组元素,low就会等于n,n是数组越界后的第一个元素,如果它刚好是要查找的值呢??展开作者回复: 谢谢指正 我稍后改下
- 菜鸡程序员2018-12-07 4
1.如果不知道分界点,找寻分界点没有意义,不如直接遍历。
2.如果知道分界点,查看在哪一边,然后二分法,或者偏移量计算,二分法
老师,我今天这种可以吗:
/**
* 功能描述:查找第一个大于等于给定值的元素
*
* @param null
* @return
* @author xiongfan
* @date 2018/12/7 9:43:00
*/
public static int getFirstGreaterValue(int[] array,int value) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = low + (high - low) >> 1;
if (array[mid] < value) {
low = mid + 1;
} else if (array[mid] > value) {
high = mid - 1;
} else {
if (mid == 0 || array[mid - 1] < array[mid]) {
return mid;
}
high = mid - 1;
}
}
return low>array.length-1?-1:low;
}
/**
* 功能描述:查找最后一个小于等于给定值的元素
*
* @param null
* @return
* @author xiongfan
* @date 2018/12/7 10:03:00
*/
public static int getLastLessValue(int[] array,int value) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = low + (high - low) >> 1;
if (array[mid] > value) {
high = mid - 1;
} else if (array[mid] < value) {
low = mid + 1;
} else {
if (mid > array.length-1 || array[mid] < array[mid + 1]) {
return mid;
}
low = mid + 1;
}
}
return high<0?-1:high;
}展开 - 姜威2018-11-03 4总结:二分查找(下)
一、四种常见的二分查找变形问题
1.查找第一个值等于给定值的元素
2.查找最后一个值等于给定值的元素
3.查找第一个大于等于给定值的元素
4.查找最后一个小于等于给定值的元素
二、适用性分析
1.凡事能用二分查找解决的,绝大部分我们更倾向于用散列表或者二叉查找树,即便二分查找在内存上更节省,但是毕竟内存如此紧缺的情况并不多。
2.求“值等于给定值”的二分查找确实不怎么用到,二分查找更适合用在”近似“查找问题上。比如上面讲几种变体。
三、思考
1.如何快速定位出一个IP地址的归属地?
[202.102.133.0, 202.102.133.255] 山东东营市
[202.102.135.0, 202.102.136.255] 山东烟台
[202.102.156.34, 202.102.157.255] 山东青岛
[202.102.48.0, 202.102.48.255] 江苏宿迁
[202.102.49.15, 202.102.51.251] 江苏泰州
[202.102.56.0, 202.102.56.255] 江苏连云港
假设我们有 12 万条这样的 IP 区间与归属地的对应关系,如何快速定位出一个IP地址的归属地呢?
2.如果有一个有序循环数组,比如4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法?展开 - 狼的诱惑2018-10-31 4@老师,请老师或其他高人回复指教
/**
* 例如: 4 5 6 1 2 3
* 循环数组的二分查找 总体时间复杂度O(n)
*/
public static int forEqualsThan(int[] arr, int num) {
if (arr[0] == num) {
return 0;
}
int length = arr.length;
int low = 0;
int high = length - 1;
//找到循环节点
for (int i = 0; i < length; i++) {
if (i == length - 1) {
if (arr[i] > arr[0]) {
low = i;
high = 0;
break;
}
} else {
if (arr[i] > arr[i + 1]) {
low = i;
high = low + 1;
break;
}
}
}
//判断第一个节点的大小位置,确定low和high的值,转变为正常有序的二分查找
if (arr[0] < num) {
high = low;
low = 0;
}
if (arr[0] > num) {
low = high;
high = length - 1;
}
while (low <= high) {
int index = low + ((high - low) >> 1);
if (arr[index] > num) {
high = index - 1;
}
if (arr[index] < num) {
low = index + 1;
}
if (arr[index] == num) {
return index;
}
}
return -1;
}展开 - 勤劳的小胖...2018-10-27 31. 先二分遍历找到分隔点index,特征是<pre, >=next;
2. 把数组分成二个部分,[0,index-1], [index,length-1];
3. 分别使用二分查找,找到给定的值。
时间复杂度为2*log(n). 不确定有什么更好的办法。展开 - komo01042018-10-26 3给原来的index加上偏移量。
比如原来的二分查找代码从0开始到n-1结束,现在为x到x - 1 (即n-1+x-n)。
x为开始循环处的索引,例子里为3 (1所在索引)。需要扫描一遍数组找到x,复杂度O(n)。其余和普通二分查找一样,需要多判断index not out of bound。如果索引超过n了要减n。
总的复杂度还是O(n)展开 - 毅仔2018-12-23 2第一次见到逻辑这么清晰的二分查找代码,已经被老师俘获了,太优雅了
- QFann2018-12-18 2public int search(int[] nums, int target) {
if(nums.length ==0) return -1;
if(nums.length ==1){
if(nums[0] == target) return 0;
else return -1;
}
int low = 0;
int high = nums.length - 1;
int index = subIndex(nums,low,high);
if(index != -1){
int val = binarySearch(nums,low,index,target);
if (val != -1) return val;
return binarySearch(nums,index+1,high,target);
}
return binarySearch(nums,low,high,target);
}
public static int subIndex(int [] nums,int low,int high){
while (low <= high){
int mid = low + ((high - low )>> 1);
if(nums.length < 1) return -1;
if(nums[mid] > nums[mid+1]) return mid;
else if( nums[mid] < nums[low] ) high = mid ;
else if (nums[mid] > nums[high]) low = mid ;
else return -1;
}
return -1;
}
public static int binarySearch(int[] nums,int low,int high,int target){
while (low <= high){
int mid = low + ((high - low)>>1);
if(nums[mid] == target) return mid;
else if (nums[mid] < target) low = mid + 1;
else high = mid -1;
}
return -1;
}展开 - 晓杉2018-11-16 2老师,我有一个疑问。
使用二分查找的前提是有序数组。
对于本节IP地址问题,我们先进行排序再进行查找,我理解应该时间复杂度是排序平均O(nLogn)再加上二分查找O(logn)
比单纯的顺序遍历O(n)要慢许多了。
是不是实际中,这种无序情况直接使用了顺序遍历查找呢?展开 - Monday2018-10-29 2二分的四种变种写法。个人觉得都是分三种情况进行讨论,再多注意判断边界值,三种情况为:
a[mid]<value
a[mid]=value
a[mid]>value;
思考题:自己思考了一小段时间没有好的思路,就各学友的留言,亲自实现了Smallfly的方法三,感觉比较好!谢谢!展开 - 朱坤2019-02-25 1置顶的同学的思路一,即先找分界再判断在哪个数组,再二分,其实是可以做到O(Log N)的,找分界的点的规则就是找到首个小于a[0]的元素,思路用老师4个转换问题的解法就可以。按评论做了下leetcode33题,感觉会比较老师给的思考题描述清晰。。因为老师说的找问题,没有明确有几组循环数组。。展开
- 牛顿的苹果...2019-01-31 1思考题:
可以考虑将数组分为N个有序数组,分别进行二分查找。
代码实现:
public int circleBinarySearch(int[] a, int value){
int low = 0, high=0;
for(int i=0;i<a.length-1;i++){
//找到有序数组的下标
if(a[i]<a[i+1]){
high=i+1;
}else{
//有序数组到顶,二分查找
int i1 = binarySearch(low, high, a, value);
if(-1 != i1){
return i1;
}else{
low = high+1;
}
}
//high已经到最后一个位置
if(a.length-1 == high){
return binarySearch(low, high, a, value);
}
}
return -1;
}
private int binarySearch(int low, int high, int[] a, int value){
for(;low<=high;){
int middle = low+((high-low)>>1);
if(a[middle] == value){
return middle;
}
if(a[middle] > value){
high = middle -1;
}else{
low = middle +1;
}
}
return -1;
}展开 - 疾风狂草2018-12-10 1老师,你说二分查找更适合用在“近似”查找问题,在这类问题上,二分查找的优势更加明显。这种问题链式哈希表不是更擅长吗?展开
作者回复: 哈希表是精准查找
- Jeson2018-10-28 1#查找第一个值等于给定值的元素
def bsearchFirst(nums, val):
low, high = 0, len(nums) - 1
while low <= high:
mid = low + ((high - low) >> 1)
if nums[mid] >= val:
high = mid - 1
else:
low = mid + 1
if nums[low] == val:
return low
else:
return None
#查找最后一个值等于给定值的元素
def bsearchLast(nums, val):
low, high = 0, len(nums) - 1
while low <= high:
mid = low + ((high - low) >> 1)
if nums[mid] <= val:
low = mid + 1
else:
high = mid - 1
if nums[high] == val:
return high
else:
return None
#查找第一个大于等于给定值的元素
def bsearchFirstLargerEqual(nums, val):
low, high = 0, len(nums) - 1
while low <= high:
mid = low + ((high - low) >> 1)
if nums[mid] >= val:
high = mid - 1
else:
low = mid + 1
if nums[low] >= val:
return low
else:
return None
#查找最后一个小于等于给定值的元素
def bSearchLastsmallerEqual(nums, val):
low, high = 0, len(nums) - 1
while low <= high:
mid = low + ((high - low) >> 1)
if nums[mid] <= val:
low = mid + 1
else:
high = mid - 1
if nums[high] <= val:
return high
else:
return None
#循环数组的二分查找
def bSearchRecycle(nums, val):
n, offset = len(nums), 3
low, high = 0, n - 1
while low <= high:
mid = low + ((high - low) >> 1)
midIdx = (mid + offset) % n
if nums[midIdx] == val:
return midIdx
elif nums[midIdx] < val:
low = mid + 1
else:
high = mid - 1
return None
if __name__ == '__main__':
nums = [0, 0, 2, 2, 3, 3]
val = 1
print(bSearchLastsmallerEqual(nums, val))
nums = [4, 5, 6, 1, 2, 3]
val = 3
print(bSearchRecycle(nums, val))展开 - 锐雨2018-10-27 1关于循环有序数组的问题,假设array无重复元素的话,我们可以先二分法将array分成两个递增数组,再分别采用二分法。有不妥之处忘赐教哦, java:
public static int search(int x, int[] array) {
if (null == array || array.length == 0) {
return -1;
}
/** Step1. 先找到循环队列新一轮从小变大的起始位置*/
int low = 1;
int high = array.length - 1;
int mid;
int firstVal = array[0];
/*到firstVal之后第一个<firstVal的position */
int dividePos = -1;
while(low <= high) {
mid = low + ((high - low)>>1);
if (array[mid] > firstVal) {
low = mid + 1;
} else {
if (mid == 1 || array[mid - 1] > firstVal) {
dividePos = mid;
break;
} else {
high = mid -1;
}
}
}
/** Step2. 对dividePos两边分别进行二分搜索 */
int targetPos = -1;
if (dividePos >= 1) {
targetPos = bSearch(x, array, 0, dividePos - 1);
if (-1 != targetPos) {
return targetPos;
} else {
targetPos = bSearch(x, array, dividePos, array.length - 1);
};
} else {
targetPos = bSearch(x, array, 0, array.length - 1);
}
return targetPos;
}
/** 普通的二分搜索 */
public static int bSearch(int x, int[] array, int low, int high) {
if (null == array || array.length == 0 || low < 0 || high >= array.length) {
return -1;
}
int mid;
while(low <= high) {
mid = low + ((high - low)>>1);
if (array[mid] > x) {
high = mid - 1;
} else if (array[mid] < x) {
low = mid + 1;
} else {
return mid;
}
}
return -1;
}展开